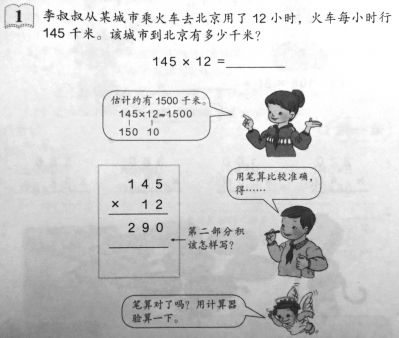
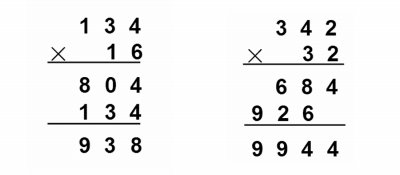145×2＝290（千米）　　先算2小时行了多少千米

　　145×10＝1450（千米）  再算10小时行了多少千米

　　290＋1450＝1740（千米） 两部分加起来算12小时行了多少千米

　　苏霍姆林斯基说过：“在人的心灵深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者、探索者，而儿童的精神世界中这种需要特别强烈。”所以在笔者提出如何计算“145×12”的准确结果时，有的学生尝试用口算的方法计算，也有的学生尝试用笔算的方法进行计算。

　　3. 笔算

　　笔算无疑是学生解决问题中常用的、便捷的计算方法之一，探索算法、理解算理是教学的重点。而小学运算内容的编排是螺旋上升的，各阶段内容之间虽然由于数位的增多，进位或退位等问题逐渐增加难度，但其中的基本算理、算法都是相通的。于是，笔者在复习引入部分和学生一起回忆两位数乘两位数的笔算的算法和算理后，有的学生就会想到把两位数乘三位数的笔算方法迁移到三位数乘两位数的笔算，从而尝试笔算145×12。

　　145

　　× 12

　　290→145×2＝290（千米）先算2小时行了多少千米

　　1450→145×10＝1450（千米） 再算10小时行了多少千米

　　1740→290＋1450＝1740（千米）两部分加起来算12小时行了多少千米

　　在沟通口算和笔算之间的关系的过程中，进一步理清算理和算法之间的关系，将学生由简单的会计算转向深入理解算法背后所蕴含的道理的层次。

　　在倡导算法多样化，让学生充分感受不同的思维方式、计算方法的前提下，需要进行算法的必要优化，才能使学生不至于处于茫然不知所措之境界。通过比较，让学生明确：估算能够估计计算结果的上界或者下界；口算无法进行大数目计算。复杂的计算只能分解为多个小数目的简便计算，短时记忆无法记住多个简单计算的临时结果，需要把各个环节的计算过程记录下来，这便产生了竖式。所以，当数据比较大时，三位数乘两位数用笔算比口算简便。

　　三、重视运算法则的归纳与提炼

　　关于运算法则，对于教过旧教材的教师来说也许不陌生，它常常是教师授课的重点之一。教材重视对结论的总结呈现，直接清晰、完整地概括出运算法则。而新课标实验教材则充分体现学生自主、合作、探索的过程。如在学习三位数乘两位数的笔算例题后，教材（如下图）并没有对三位数乘两位数的笔算方法进行总结。这种编排，如果教师没有认真研读教材，领悟意图，是很难在课堂实践中落实“法则”教学的。正是这种原因，造成很多学生纵然理解了算理，明白了算法，但没有必要的概括与提炼，必然影响运算能力的提高。所以，在学习了三位数乘两位数的笔算方法，同时明白了其算理后，我让学生自主归纳与概括三位数乘两位数的笔算方法。通过总结，有利于学生更好地掌握三位数乘两位数的笔算方法。

　　四、重视算法的落实

　　运算技能不是一朝一夕就能形成的，需要一个循序渐进、扎实有效的训练巩固过程。在运算教学中，安排一定数量的练习，完成一定数量的习题是必不可少的。教师不但要精于设计练习，也要布置一定量的同步练习，还要设置形式不同的变式练习，让学生体会算法的不同应用，掌握运算技能，提高运算能力。

　　如在学习了三位数乘两位数的笔算方法后，我设计了以下练习：

　　第一关：我能算。

　　134（不进位）   237（进位）

　　× 12　　　　　　　　 × 82

　　第二关：我能改：说出下面计算中的错误，并改正过来。

　　第三关：我能选。

　　（1）在计算234×35的时候，2×5表示（　　 ）

　　A.2×5  B.20×5  C.200×5  D.200×50

　　（2）下面（   ）算式中2×5表示的意思是200×50

　　A. 209×15　　  B. 209×52  

　　C. 325×52　　  D. 152×5

　　第四关：我能用。

　　学校要为各班新购买一套百科全书。全校共36个班，购买这些新书一共要花多少钱？

　　129元/套

　　在练习设计中，需要充分考虑学生运算技能的培养与发展。第一关复习三位数乘两位数的笔算方法。第二关，通过辨析计算，有助于学生进一步巩固三位数乘两位数的笔算方法，同时提醒学生笔算中要注意“用第二个因数的十位乘第一个因数的个位时，积对准十位”“进位”等要点。第三关和第四关的练习，目的是引导学生进一步掌握多位数乘法的计算方法，理解乘法运算的基本原理，同时让学生用所学知识解决实际问题。让学生体验到生活离不开数学，数学来源于生活，并服务于生活；体会到数学就在身边，感受到数学的趣味和作用，体验到数学的魅力。

　　在运算教学中，教师不但要让学生自主探究、发现、总结其算法，也要让学生明白其算理，并归纳与提炼算法，还要再通过适量的练习巩固计算方法，掌握运算技能，从而培养和提高学生的运算能力。

　　责任编辑　罗　峰