现象二:教师“默认”“用结论证结论”

　　如果说，学生犯循环论证的错误是“情有可原”———想偷懒(不计算)、逻辑思维不成熟等。那么，教师会怎样处理呢?部分教师是这样处理的:

　　1.选择有代表性的例子，让学生板书在黑板上(或学生说，教师板书);

　　2.学生从左至右依次板书(或教师按照学生说的过程从左至右依次板书);

　　3.观察所有算式，找相同点;4.总结规律，形成结论。

　　不难看出，以上教学，教师默认了学生的思维错误。课后，本人找执教教师访谈，或者与所有听课教师交流，发现造成这一现象的原因主要有两方面:一是教师自身根本没有意识到逻辑错误所在，即自身本体性知识的缺失;二是部分教师只重知识的教学，忽略思维方法的引导。部分教师表示，当时感觉似乎有点不妥，但是急于想得出结论，也就没太在意，一带而过了。

　　也许以上教师没有意识到:培养学生严谨、科学的研究态度以及符合逻辑的思维方式，远比得到一个结论、记住一个知识点重要。不说长远，仅就小学数学而言，此类课占有一定课时数和学习量，其学习方式和思路也基本一致，因此，笔者建议:教师应该在这一类课的起始课，即加法交换律的教学时，做好充分的研究和设计，注意思维方法和学习方式的渗透和培养，为学生学习这一类课打好基础。

　　课例二:平行四边形的面积

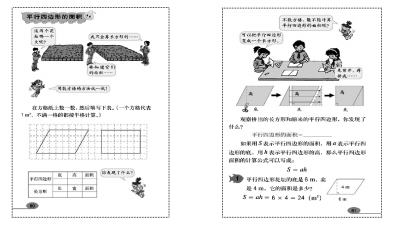
　　“平行四边形的面积”一课的教学，通常都会安排数方格(图3)环节。

　　数方格计算面积，其作用有以下几点:一是可以直观计量，且基于学生原有认知和经验(学生在学习长方形、正方形的面积计算时已经使用过);二是暗示了长方形和平行四边形两者之间的联系;三是通过数据，可以为学生猜想平行四边形面积计算公式提供依据(或者为证明猜想提供例证)。基于以上分析，我们可以知道，数方格的教学，是为探索平行四边面积计算公式所进行的必要的铺垫，但无论如何:此环节没有得出公式，更不可能运用公式。然而，听课中，笔者多次在此环节遇到以下问题:

　　教师布置数方格任务，学生开始独立或小组合作数方格，完成表格填写。

　　此时，笔者观察到:学生填写表格时，通常只数“底(长)”和“高(宽)”的数据，面积的数据则通过计算得出。以下是笔者和学生的对话:

　　笔者:XX同学，平行四边形的面积是24平方厘米，你怎么知道的?

　　生:算的，6X4=24。

　　笔者:为什么用6X4呢?

　　生:6是底，4是高，底乘高。

　　笔者:你认为用底乘高就可以算出平行四边形的面积?

　　生:嗯!

　　以上是学生在认知上存在的思维逻辑。形成这种认知有以下几种情况:一是学生已经先学，明确知道平行四边形的面积计算公式是底乘高;二是受前面环节“猜想”的影响，把“猜想”当成了结论;三是受长方形面积计算的影响，直接进行迁移!不管是哪种情况，在这里，学生始终没有明白的思维逻辑是:平行四边形的面积计算公式需要通过自我探索、证明才能形成结论。对于学生的这一思维逻辑，教师又是如何处理的呢?以下是汇报环节的教学片断(学生数方格之后，教师组织汇报交流):

　　师:谁来说说数的结果?

　　生:我发现平行四边形的底是6厘

　　米，高是4厘米，面积是24平方厘米。

　　师:长方形呢?

　　生:长方形的长是6厘米，宽是4厘米，面积是24平方厘米。

　　师:同学们，你们数的和他一样吗?生:一样。

　　师:对的，非常好!那你们观察一下表格中的数据，有什么发现?

　　生:我发现:平行四边形的面积等于底乘高。

　　……

　　很显然，以上片段教师并没有纠正学生的思维过程。那么，教学中该如何处理比较妥当呢?笔者建议:一是学生汇报后，教师要强调并确认面积是数出来的。可以在学生汇报的基础上，问学生:大家都数了吧?我们一起数一数。然后带着学生，通过课件演示，重数一次。第二，纠正个别学生的逻辑错误。利用课堂生成资源(如果怕伤害学生自尊，也可以虚拟一个人物)，将采用计算得到面积的思维暴露给学生，让学生自己辨析，在辨析中明确问题所在，最后得到正确思维方法。

　　以上两个课例中提到的逻辑错误，是笔者在多年听课中经常遇到的问题，期望通过以上分析，能让教师建立正确的认识，避免此类问题重复发生。在教学中，其他逻辑错误同样存在，如以偏概全、偷换概念等。在此，也呼吁教师多了解和学习逻辑学知识，提高自身素养，在教学中注意遵循教学的序、知识的序、思维的序，帮助学生建立正确的思维方式和逻辑结构。

　　责任编辑