1.各数学小组都推荐一件“优秀作品”并由制作者在课堂上进行展示，介绍其制作方法和注意事项，然后再由各组组长用口头表达的方式，对椭圆进行初步的描述。

　　2.分析、比较各数学小组对椭圆的描述，找出最贴切的一个，最后引出教材所给出的椭圆定义，同时，还要提出焦点和焦距的概念。在这一基础上，引导学生利用自己所作的椭圆图形，按照求轨迹方程的固定步骤，对椭圆的标准方程进行推导（推导可以分焦点在x轴和y轴两种情况）：（1）在所画的椭圆上建立适当的直角坐标系，并设曲线上任意一点M的坐标为（x,y）；（2）根据题意，用等式写出动点M在曲线上的充要条件；（3）用动点坐标x和y表示上述条件，列出含x、y的方程；（4）整理并化简方程；（5）说明化简后的方程即为所求曲线的方程。

　　3.通过讲解例题、课堂练习和课后练习，加深学生对椭圆的理解，准确地判断椭圆焦点所在的轴，避免混淆焦点在x轴和y轴两种情况。

　　（四）项目检验阶段。

　　1.让学生随意地画出一个椭圆，然后测量焦距和绳长，得到相应的c值和a值后，再由c2=a2－b2求出b值，最后将a值和b值代入(a>b>0)两种标准方程，通过比较相应的图形，更好地理解椭圆焦点在x轴和y轴的两种情况。

　　2.给出特殊数值的标准方程，要求学生调整学习用具中的焦距和绳长，较为准确地画出已知方程相应的椭圆图形。

　　3.以第2点中的标准方程及相应椭圆的图形为例，深入讲解椭圆的几何性质，包括范围、对称性、顶点和离心率等内容，同时通过讲解例题、课堂练习和课后练习，加深学生对椭圆几何性质的理解。

　　四、项目驱动式教学法的应用成效

　　（一）激发学生的才智。

　　笔者在使用项目驱动式教学法过程中，发现学生在动手制作学习用具时表现出很强的主观能动性，最大限度地发挥了自身的聪明才智，他们思考问题、解决问题的独特思维，使笔者惊喜不已。

　　实例之一：学生制作学习用具，除了用一般的硬纸板、铁钉和棉线，还使用了木板、塑料板、螺丝钉、图钉和吸盘等材料，制作方法各有特点，如有个别学生用螺丝钉或吸盘来确定焦点，方便取出并很容易调整焦点的位置。

　　实例之二：为了更好地比较焦点在x轴和y轴的两种椭圆，许多学生在不改变焦距和绳长的前提下，将两种情形的椭圆图形画在同一个平面直角坐标系上，这有助于加深对椭圆的理解。

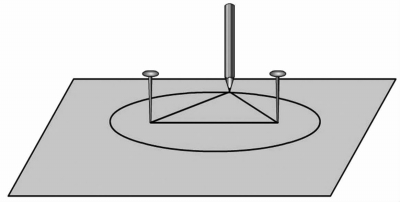
　　实例之三：如果按教材描述的方法来画椭圆，会因为细绳缠绕着铁钉，不能一笔就把椭圆完整地构勒出来，操作起来极为不便。有的学生调整了画椭圆的方法，把一根没有弹性的细绳两端系紧，形成一个环，然后把绳环套在F1和F2两点处的铁钉上，只要保证绳环长度的一半大于F1和F2之间的距离，用笔撑着绳套绕一圈，没有丝毫的阻滞就轻易地画出一个椭圆（如图2所示）。

　　（二）难以替代的作用。

　　有人质疑，为什么要浪费时间让学生制作学习用具，教师自己制作教具，效果不是更好吗？确实，教师用教具画出的图形，也许比学生更规范，但是教师只凭演示作图，并不能让每个学生体会圆锥曲线的画图原理。相反，如果预设项目进行引导，学生在学习用具的制作过程中，自然能够更好地理解圆锥曲线，并画出各种圆锥曲线的图形。此外，在最后的项目检验阶段，结合自己制作的学习用具，通过调整焦距和绳长，能够很好地体会到标准方程中a、b、c和p（抛物线）等数值在相应图形中的几何意义，这有助于学生全面掌握圆锥曲线的知识。

　　（三）符合教育的规律。

　　人类教育起源于劳动或劳动过程中所产生的需要，这是“教育的劳动起源说”所提出的观点。由于圆锥曲线的图形具有典型的几何特性，因此，在圆锥曲线的教学过程中应用项目驱动式教学法，设立动手制作的教学项目，并结合自己的劳动成果深入研究圆锥曲线，这完全符合教育的规律。

　　此外，在圆锥曲线的教学过程中，合理地应用项目驱动式教学法，事实证明是行之有效的，对中职生而言，教学的效果尤其明显：一方面，通过行为引导学生动手实践，有效地将理论知识过渡为操作项目，降低了学生学习圆锥曲线的畏难情绪；另一方面，激发了学生学习数学的热情，积极参与数学小组的学习活动，从而提高了学习质量。

　　（作者单位：东莞市信息职业技术学校）

　　参考文献：

　　[1]许杏芳.案例教学在离散数学中的应用[J].福建电脑，2007，（7）.

　　[2]张奇.项目驱动式教学在《管理信息系统》中的应用探讨[J].电脑知识与技术（学术交流），2007，（9）.

　　[3]董黎明，孟昭文，郭新.项目驱动式教学在《Linux服务器管理》课程中的应用研究[J].北京城市学院学报，2008，（1）.