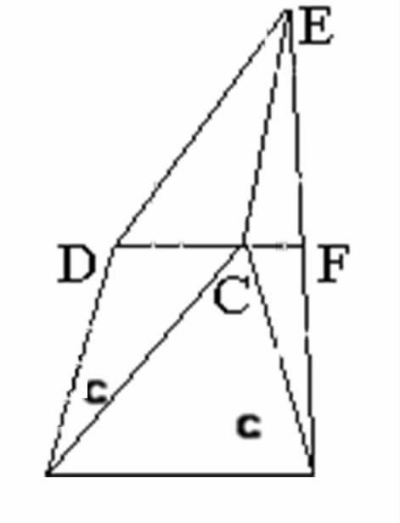
ACED是平行四边形，DC延长线交BE于 F。 

　　求证：BF＝EF。

　　方法 1：延长EC交AB于 G，易证 AGCD是平行四边形。欲证BF＝EF，只须证 C是EG中点即可。由题目条件与辅助线作法不难得此结论。（证明略）

　　方法 2：过 B作BN∥AD交DC延长线于 M，连ME。欲证BF＝ EF，只须证明四边形 BMEC是平行四边形。由已知条件和辅助线作法容易得此结论。（证明略）

　　方法 3：过 E作EN∥CD交AD延长线于 N，欲证BF＝EF，只须证明 D是梯形 ABEN的腰AN的中点即可，由已知条件易得四边形 DCEN是平行四边形，又四边形 ACED是平行四边形，可推出DN＝CE＝DA，问题得证。（证明略）

　　象这样在习题课教学中科学的启发学生同中求异时，强化一题多解，沟通了知识联系和解题思路，提高学生综合运用知识解题的灵活性，更重要的是培养了学生思维的发散性、广阔性，极大的培养了学生创造性思维的能力。

　　四、恰当引入开放题型，培养学生思维的创造性。

　　数学开放题又称数学开放型题，目前学术尚未统一定义，但是它一般具有下列特征：问题的答案，常常是不唯一的；没有现成的解题模式；在寻求解答的过程中可促进主体的认知结构改进；特别是因为答案多，入门不难，全体学生都可以参与；由于思维发散度大，教师不会采用注入式教学；最后，因为求解过程的发散性，往往题中有题，可以不断引出新的问题。因此，数学开放型题的含义，应该是条件开放或是结论开放的问题。由于数学开放题的结构包含了条件不完备或结论不确定这样一个特点，所以在教学中可以向学生提出“这个问题的结论会有多少？还有没有更好的形式？”等问题，这样有效地弥补了传统数学解题中出现的思维定势现象，实现了思维的灵活性、广阔性。开放题没有改变逻辑推理方法，但改变了逻辑推理的结果，题目的答案特别多，入门不难，全体学生都可以参与，为培养学生的创造性思维带来了新的突破。