悬念是一种学习心理机制，它是由学生对所学对象感到疑惑不解，而又想解决它产生的一种心理状态。悬念的设置，能激发学习学习动机和兴趣，使学生思维活跃、想象丰富、记忆加强，并有利于培养学生克服学习困难的意志力。教师在课堂教学中，要善于捕捉时机，恰当设悬念，以拨动学生探索新知识的心理，提高课堂教学效益。

　　1. 课前设悬念，学习添情趣

　　俗话说，良好的开端是成功的一半。教师在讲授新课前，先设置悬念，以触发学生的求知欲，产生一种非知不可的情感，形成认知“冲突”，“冲突”一旦形成，学生的注意力最集中，思维处于最积极的状态，从而更好地激发学生的学习兴趣。

　　案例1　“三角形内角和定理”是初中几何最基本的定理之一。对小学未学过几何推理但又知道结果的初中生来说，对几何推理显得无从下手、抽象难懂，为激发学生的学习兴趣，在介绍本定理的推理之前，笔者对这个定理作了如下处理：

　　师：同学们，今天我们要来探索三角形的三个内角和究竟是多少度。

　　生：１８０°。

　　师：你们是怎么知道的？

　　生：在小学时，老师教我们把三角形纸片的两个角剪下来，拼在第三个角的顶点处，得到一个平角，所以三角形的三个内角加起来是。

　　师：很好，你还记得小学做过的事。现在请大家再来剪一剪，拼一拼？好吗？

　　生（齐声）：好。

　　学生纷纷拿出剪刀和纸片（课前教师要求学生带剪刀），开始剪拼。过了大约两三分钟，全部拼好，放在桌面上。

　　师：大家都做得很好。但这个结果是通过一两次实验得出的，还不足以说明所有的三角形都有相同的结果。前面同学们已经学习了相当多的几何知识，大家能否用学过的知识来证明呢？学生们带着这个悬念，开始津津有味地探究证明方法。

　　教师在黑板上画出△ABC，要求学生说出已知与求证。

　　已知：△ABC。

　　求证：∠A+∠B+∠C=180°。

　　明确问题后，老师启发：我们不妨从结果来看一下，求证的关键在于两点：①如何提供180°；②怎样把∠A，∠B，∠C加在一起，请大家想一想，然后交流讨论。

　　学生踊跃发言：

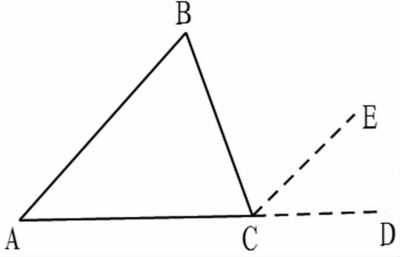
　　生1：延长BC到D，在△ABC的外部作∠BCE=∠B，这样可要证明∠ECD=∠A。（图1-1）

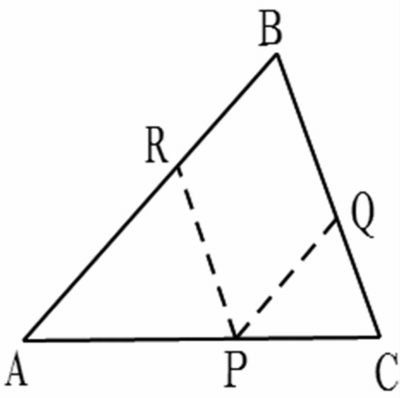
　　生2：在△ABC的边上任取一点P，过P点作PR//BC，交AB于R，PQ//AB，交BC于Q，这样也能把三个内角移到一起，而且证明也不难。（图1-2）。

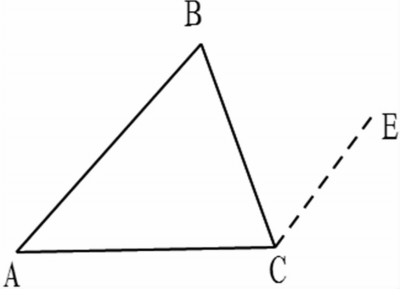
　　生3：还有一个办法：只移一个角的。这就是过点C作∠BCE=∠B，利用两直线平行同旁内角互补来证明。（图1-3）

　　师：刚才三位同学都做得很好。确实是动了脑筋，作了一番探究。看来一个问题的解决有时可有多种方法，希望同学们在做几何证明题时，从不同角度，往多方向、用多种方法或途径进行分析和解决问题，从而培养发散思维能力。

　　2. 课中设悬念，学习见深度

　　在课堂教学中，教师除了要顺理成章地进行新课讲授外，还要有目的、有意识地设置悬念，拓宽学生的思维，使学生有所思，思有所得，以达到举一反三的效果。

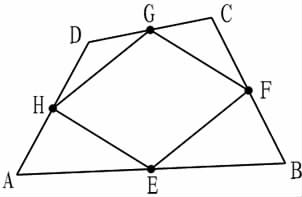
　　案例2  在学习“三角形的中位线”的应用教学中，首先请每个同学任意画一个四边形ABCD，取各边中点E，F，G，H，再依次连接EF，FG，GH，HE，试判断四边形的形状（图2-1）。对这道题目，学生应用学过的“三角形的中位线定理”就能判定四边形EFGH是平行四边形。