样例又称例子或范例，是一种能够例说或表征较为抽象的概念原理的相对具体的实体，能够展示同一类事物性质的样本或值得模仿的榜样．样例在原理学习与迁移过程中的作用是当前研究学习迁移问题的热点之一．

　　样例学习是指学习者通过研习样例而习得专家的问题解决方法的一种学习方式．“样例学习”在数学教学中扮演了十分重要的角色．数学样例是数学问题及其解答的组合体，或者是一个数学概念、公式或原理的一个具体“实体”对象．在数学教学中，教会学生懂得如何解决问题，习得问题解决技能，促进问题解决的迁移，形成有效的数学迁移，提高数学学习效率，是我们教师在教学中设计样例的目的．

　　一、精于样例问题的组织形式和呈现方式，减轻学生解决问题的负担 

　　维果茨基的最近发展区理论认为，在学生实力所能达到的水平与经过别人给予协助可能达到的水平之间有一段差距，这就是该学生的最近发展区．维果茨基的最近发展区理论在教学上具有重要的意义，教学的最佳效果产生于学生的最近发展区．它为我们的样例设计提供了坚实的理论基础．因此，我们在引导学生习得问题类型的解决方法时，要从学习记忆承受负荷的“最近发展区”出发，精设样例问题的组织形式和呈现方式．在此过程中，教师要给予学生“支架作用”的协助，选择阶梯式的方式来处理问题，将其设置成几个小问题，在内容和要求上要注意循序渐进、由易到难，同时也要注重前后问题之间知识的逻辑连续性， 用具有逐层递进关系的小问题解决大问题，从而减轻认知负荷，并从中掌握问题类型的解决方法．

　　案例一：大边相等、小边相等全等三角形对应边夹角的求法．

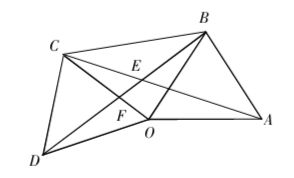
　　例：如图，△ＯＡＢ和△ＯＣＤ都是等边三角形，连结ＡＣ和ＢＤ，相交于点Ｅ，ＢＤ与ＣＯ相交于点Ｆ，连结ＢＣ．（１）求证：△ＢＯＤ≌△ＡＯＣ；（２）△ＣＦＥ∽△ＤＦＯ；（３）求∠ＣＥＤ的度数．

　　当学生完成题目后，教师要引导学生总结该题目的条件、问题、图形三方面的特征，并让学生归纳出该模型的解决方法：关键是发现大边相等、小边相等的全等三角形，找出夹角所在的三角形，再利用两线相交对顶角相似的基本图形，找出其相似三角形，得到夹角的相似对应角，进而求得夹角的度数．

　　设计意图：此类型的最后目的是求全等三角形对应边的夹角．教师通过将大问题降低难度，分解成几个小问题，给学生架了一个阶梯，帮学生迅速解决问题，更重要的是学生通过经历问题类型的解决过程，能较轻易地找到问题的解决方法，减轻了认知负荷，提高了学习效率．

　　二、精于渗透几何基本图形，提高学生顺向推理的问题解决技能

　　问题解决过程中，“手段—目的”分析策略的应用会抑制图式的获得，而自动化的图式在工作记忆中是作为一个组块存储的，就像计算机传输打包处理的压缩文件一样，会大大减少工作记忆的负荷．在数学学习中，我们要引导学生加强对图式、产生式条件部分的认知，将零碎的图式、产生式模块化，使学生发展出顺向推理的问题解决技能，即获取自动化的图式和产生式系统，从而减轻认知负荷，加快认知速度，提高学习的效率．

　　几何图形千变万化，初三的学生学习完四边形这一章后，面对几何题目常常束手无策、一筹莫展．针对这一现象，我们可以采用“基本图形法”来帮助学生提高分析复杂图形的能力．

　　平面图形可以通过各种不同图形的组合而产生无穷变化，但任何一个图形往往都是由一个或若干个最基本的图形组合而成的， 因此可以从研究基本图形的性质、应用范围入手， 来分析或解决复杂问题，这种方法就是基本图形法．它可以有效地揭示规律， 克服学生“几何难学”的恐惧心理，也使平面几何教学摆脱了困境．

　　案例二：几何图形的拆分．

　　例１：四边形ＡＢＣＤ中，对角线ＡＣ＝ＢＤ，Ｅ、Ｆ、Ｇ、Ｈ分别是ＡＢ、ＢＣ、ＣＤ、ＤＡ的中点．判断：四边形ＥＦＧＨ是何种特殊四边形？请你证明．结论： 的中点四边形是菱形．

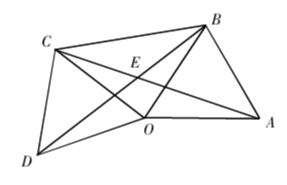
　　例２：如图，△ＯＡＢ和△ＯＣＤ都是等边三角形，连结ＡＣ和ＢＤ，相交于点Ｅ，连结ＢＣ．求证：ＡＣ＝ＢＤ．

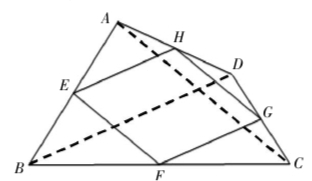
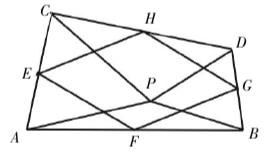
　　例３：如图，Ｐ是线段ＡＢ上方的一点，在ＡＢ的同侧作△ＡＰＣ和△ＢＰＤ，使ＰＣ＝ＰＡ，ＰＤ＝ＰＢ，∠ＡＰＣ＝∠ＢＰＤ，连接ＣＤ，点Ｅ、Ｆ、Ｇ、Ｈ分别是ＡＣ、ＡＢ、ＢＤ、ＣＤ的中点，顺次连接Ｅ、Ｆ、Ｇ、Ｈ．猜想四边形ＥＦＧＨ的形状，并证明．