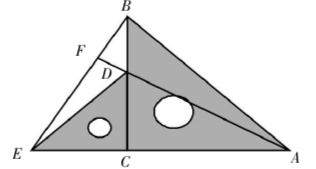
设计意图：先设计例１、例２两道简单的题目，目的是让学生记住其基本图形的性质和特点；然后再出示例３这道比较复杂的题目， 让学生对这道题目的图形进行适当地分析和提炼，辨认出例１、例２的基本图形， 或者构造出它们的基本图形；从而根据基本图形的性质， 择取有用的信息和结论， 迅速地找到证题思路和证题方法，让学生感受基本图形对几何证题的作用，培养学生对几何图形的拆分能力，提高学生顺向推理的问题解决技能．

　　三、精于变式题组的设计，提高学生问题解决的迁移能力

　　在样例学习中至少应该向学习者提供两个以上的样例，学习效果才会较好．样例中变式的增加可能促进图式和迁移的获得，因此设计出有利于学生把握问题性质特征的系列样例，促进学生的问题解决迁移是教师教学设计的主要手段．

　　我们可以先对样例中某个关键的表面特征进行变异，引起学生对该特征的重视，并对问题的类型进行类比，从而找到解决问题的恰当方法．然后教师再引导学生利用表面相似这个“相同中的不同”找出源问题所要体现的知识点和思想方法．与此同时，问题类型的相似使得学生模仿这种解题思路，并运用于具体的新问题中．而且学生将逐渐变得有心得和自信，能够逐步摈弃表面特征继而转入根据结构特征对问题进行类比、归纳，促进图式和迁移的获得．

　　案例三：判断全等或相似的两个直角三角形斜边互相垂直的变式设计．

　　例１：如图，把两个含有４５°角的直角三角板如图放置，点Ｄ在ＢＣ上，连结ＢＥ，ＡＤ，ＡＤ的延长线交ＢＥ于点Ｆ． 试猜想ＡＤ与ＢＥ的位置关系，并给出证明．

　　教师引导学生分析图式特征，找到相似的类型问题（案例一之例题），运用其解决原理解决上例，并引导学生明确：证两对应斜边垂直，关键是找出斜边夹角所在的三角形，再利用两线相交对顶角相似的基本图形，找出其相似三角形．

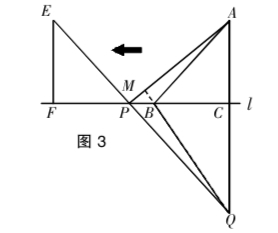
　　例２：如图３，△ＡＢＣ的边ＢＣ在直线ｌ上，ＡＣ⊥ＢＣ，且ＡＣ＝ＢＣ；△ＥＦＰ的边ＦＰ也在直线ｌ上，ＥＦ⊥ＦＰ，且ＥＦ＝ＦＰ·ＥＰ的延长线交ＡＣ的延长线于点Ｑ，连结ＡＰ，ＢＱ．试猜想的ＢＱ与ＡＰ的数量关系和位置关系，并给出证明．

　　分析：证夹角∠ＰＭＢ所在三角形的对顶角三角形相似 ．

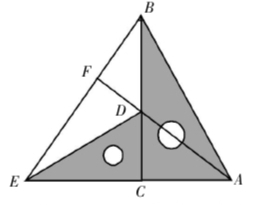
　　例３：如图，把两个含有３０°角的直角三角板如图放置，点Ｄ在ＢＣ上， 连结ＢＥ，ＡＤ，ＡＤ的延长线交ＢＥ于点Ｆ．问ＡＦ与ＢＥ是否垂直？并证明． 

　　条件的改变不代表目的的改变，４５°的三角板变为３０°的三角板同样给出信息：两对直角边的比例：■＝■，将该比例进行变形：■＝■，可找到△ＢＥＣ∽△ＡＤＣ，得∠ＥＢＣ＝∠ＤＡＣ，同样达到证对顶角三角形相似的目的．

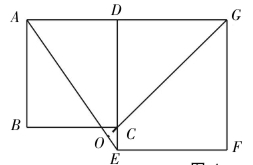
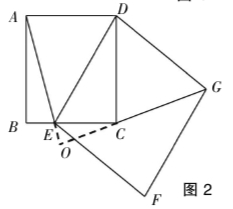
　　例４：如图１，已知正方形ＡＢＣＤ的边ＣＤ在正方形ＤＥＦＧ的边ＤＥ上，连接ＡＥ、ＧＣ．（１）试猜想ＡＥ与ＧＣ有怎样的位置关系，并证明你的结论．（２）将正方形ＤＥＦＧ绕点Ｄ按顺时针方向旋转，使点Ｅ落在ＢＣ边上，如图２， 连接ＡＥ和 ＧＣ．你认为（１）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．

　　分析：想办法证两斜边夹角所在三角形的对顶角三角形相似．

　　设计意图：①例２通过改变题目的表面特征，进一步强化了学生识别模型的能力和问题解决方法的运用，用“量”的积累达到知识的记忆与巩固．②例３通过改变题目的结构特征，保留了源问题的本质特征，帮助学生将问题的本质特征从图形中提炼出来，达到了对“源问题”质的理解．③例４的综合变式练习，通过对数学模型的拓展、延伸，能完全促进学生图式和迁移的获得，促进了有效学习的发生．

　　“样例”以其显著的优点，以及其在解决问题中的重要作用在教学中颇受青睐．数学样例清除了抽象的数学理论架构和人们认知之间产生的隔阂，将所教学的知识串起来，易化了知识的获得过程，大大减轻了学生的认知负荷，让学生好学、好记、好用，提高他们的学习兴趣，从而促进学生问题解决技能的获得及学习的有效迁移，使数学学习事半功倍．

　　责任编辑　罗　峰