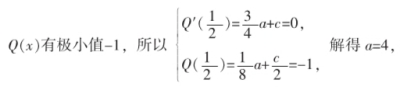函数、导数、不等式三者之间有着紧密的联系．导数是研究函数性质的有力工具， 尤其是处理高次函数、分式函数、根式函数、指数函数、对数函数、三角函数以及它们的复合型函数问题时，更能体现其应用价值、思维价值和工具价值．不等式贯穿于函数的单调性、极值、最值等问题之中，同时导数又为一些用传统方法难以处理的不等式问题提供了求解的新思路和新途径．可以说，导数的引入，拓宽了高考对函数与不等式问题的命题空间，以致在近年来的高考中，函数、导数、不等式的交汇成为考查的重点、难点和创新点．

　　考点１． 函数基本知识及其联系问题

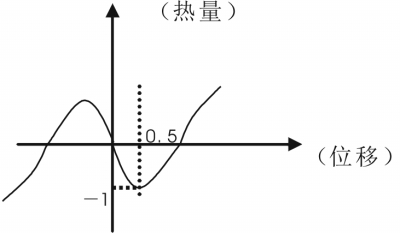
　　例１． 已知某质点在运动过程中，热量Ｑ随位移ｘ变化的规律是Ｑ（ｘ）＝ａｘ３＋ｂｘ２＋ｃｘ＋ｄ，其图像关于坐标原点对称，如图１是其图像的一部分，求Ｑ（ｘ）的解析式．

　　［解析］∵Ｑ（ｘ）的图像关于坐标原点对称，∴Ｑ（－ｘ）＝－Ｑ（ｘ），

　　即－ａｘ３＋ｂｘ２－ｃｘ＋ｄ－ａｘ３－ｂｘ２－ｃｘ－ｄ，∴ｂ＝ｄ＝０．

　　因此Ｑ（ｘ）＝ａｘ３＋ｃｘ，Ｑ′（ｘ）＝３ａｘ２＋ｃ．

　　由图像可知，当ｘ＝1/2时，

　　ｃ＝－３，Ｑ（ｘ）＝４ｘ３－３ｘ．

　　［点评］函数基本知识主要包括函数的奇偶性、单调性、周期性、对称性、图像、极值、最值等．本题以物理知识为背景，给出质点的运动轨迹（即原函数的图像），融函数的奇偶性、导数、极值的考查于一体，从原函数图像上发现其极值点而得到Ｑ′（1/2）＝０是解题的关键． 

　　考点２． 函数图像的切线及其联系问题

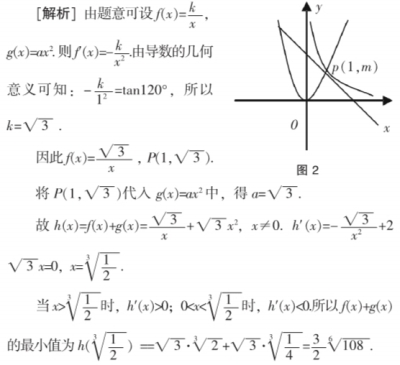
　　例２． 反比例函数ｆ（ｘ）（ｘ＞０）和二次函数ｇ（ｘ）的图像如图２所示， 在它们交点Ｐ处的反比例曲线的切线的倾斜角为１２０°，求ｆ（ｘ）＋ｇ（ｘ）的最小值．　　　　   

　　［点评］本题考查函数的图像、函数的解析式和图像的切线，利用导数的几何意义（ｆ′（１）＝ｔａｎ１２０°）确定待定系数ｋ是解题的关键．函数ｆ（ｘ）在ｘ０处的导数ｆ′（ｘ０）的几何意义就是曲线ｙ＝ｆ（ｘ）在点（ｘ０，ｆ（ｘ０））处的切线斜率，以此点为切点的切线方程是ｙ－ｆ（ｘ０）＝ｆ′（ｘ０）（ｘ－ｘ０）．

　　考点３． 函数与数列的交汇问题

　　例３． 已知函数ｆ（ｘ）＝２ｘ－２－ｘ，数列｛ａｎ｝满足ｆ（ｌｏｇ２ａｎ）＝－２ｎ．