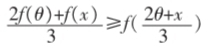［点评］本题考查了复合函数、数列以及函数单调的导数式条件．数列是特殊的函数，将ａｎ＝ｇ（ｎ）视为ｎ的函数，利用函数导数的符号判断数列｛ａｎ｝的单调性．

　　考点４． 函数图像的公切线问题

　　例４． 设函数 ｆ（ｘ）＝ｅｘ的反函数为ｇ（ｘ），点Ｐ（ｘ１，ｙ１），Ｑ（ｘ２，ｙ２）分别为函数ｆ（ｘ）的图像Ｃ１和ｇ（ｘ）的图像Ｃ２上的两个动点， 过Ｐ、Ｑ的直线为ｌ，当ｌ为曲线Ｃ１、Ｃ２的公切线时，求ｘ１，ｘ２满足的关系以及ｘ１的取值范围．

　　［点评］本题是超越型函数图像的公切线问题，用传统方法难以求解． 这里根据导数的几何意义得到公切线ｌ的两种表达式，从而构建方程，获得ｘ１，ｘ２的关系， 进一步求出ｘ１的取值范围．一般地，如果直线ｌ切曲线ｙ＝ｆ（ｘ）和ｙ＝ｇ（ｘ）分别于点Ｐ（ｘ１，ｙ１），Ｑ（ｘ２，ｙ２），则ｌ有两种表示方法：ｙ－ｆ（ｘ１）＝ｆ′（ｘ１）（ｘ－ｘ１）和ｙ－ｇ（ｘ２）＝ｇ′（ｘ２）（ｘ－ｘ２）， 即它们表示同一条直线，我们常常以此构建方程组ｆ′（ｘ１）＝ｇ′（ｘ２），ｆ（ｘ１）－ｘ１ｆ′（ｘ１）＝ｇ（ｘ２）－ｘ２ｇ′（ｘ２）来解决公切线问题．

　　考点５． 超越型不等式的证明问题

　　例５． 设ｆ（ｘ）＝ｘ－ｓｉｎｘ，若ｘ∈［０，?仔］，?兹∈（０，?仔），试证明

　　［点评］本题中的超越型不等式用传统方法难以证明，导数为这类问题的研究和解决提供了新思路． 由于导数在这类问题中的应用往往是隐性的，需要我们去创造条件、去构造模式（主要是构造新函数，此题中就是函数ｇ（ｘ）），这就常常导致我们只重视用传统方法思考，而忽视导数的应用． 不等式的证明除常见的比较法、分析法、综合法、反证法外，构造函数、利用导数知识处理是一种非常重要的方法．在涉及指数、对数、分式、三角等复杂的不等式证明问题中，有着其他方法不可比拟的优越性，因此要重点关注．

　　类型６． 含参数的恒成立不等式问题

　　例６． 已知函数ｆ（ｘ）＝a/3ｘ３－3/2ｘ２＋（ａ＋１）ｘ＋１，其中ａ为实数． 若不等式ｆ′（ｘ）＞ｘ２－ｘ－ａ＋１对任意ａ∈（０，＋∞）都恒成立，求实数ｘ的取值范围． 

　　［解析］因为ｆ′（ｘ）＝ａｘ２－３ｘ＋（ａ＋１），所以ｆ′（ｘ）＞ｘ２－ｘ－ａ＋１就是ａｘ２－３ｘ＋（ａ＋１）＞ｘ２－ｘ－ａ＋１，即（ｘ２＋２）ａ－２ｘ－ｘ２＞０．

　　令ｇ（ａ）＝（ｘ２＋２）ａ－２ｘ－ｘ２，则ｇ′（ａ）＝ｘ２＋２＞０，ｇ（ａ）在ａ∈（０，＋∞）上单增，（ｘ２＋２）ａ－２ｘ－ｘ２＞０在ａ∈（０，＋∞）恒成立?圳ｇ（０）≥０， 所以－２ｘ－ｘ２≥０，解得－２ｘ≤ｘ≤０，即为实数ｘ的取值范围．

　　［点评］本题涉及整式函数型恒成立不等式， 主要考查多项式函数的求导法则、导数与函数单调性的关系． 一要注意三次函数的导函数则是二次函数， 二次函数是我们熟悉的模型，这是导数的降次功能． 二要注意构造新函数ｇ（ａ），活用导数知识求出ｇ（ａ）的值域，顺利实现解题目标．一般地，不等式ｆ（ｘ）＜ｋ（ｋ为实数）在ｘ∈Ｉ上恒成立?圳ｆｍａｘ＜ｋ（ｘ∈Ｉ）；不等式ｆ（ｘ）＞ｋ（ｋ时恒成立）在 ｘ∈Ｉ时恒成立?圳ｆｍｉｎ＞ｋ（ｘ∈Ｉ）．求解此类问题最常见的方法是函数最值法，即构造出相应的辅助函ｆ（ｘ），利用上述结论处理． 本题不等式（ｘ２＋２）ａ－２ｘ－ｘ２＞０在ａ∈（０，＋∞）恒成立?圳ｇ（ａ）＝（ｘ２＋２）ａ－２ｘ－ｘ２在（０，＋∞）上的最大值大于零?圳ｇ（ａ）≥０．