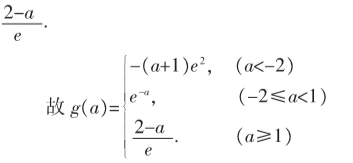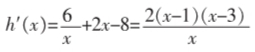例７． 函数ｆ（ｘ）＝ｘ２ｅａｘ，其中ａ∈Ｒ．

　　（１）当ａ＝１时，求函数ｆ（ｘ）的单调区间；

　　（２）若函数ｆ（ｘ）在（－∞，－１］上递增，求实数ａ的取值范围．

　　［解析］（１）ｆ（ｘ）＝ｘ２ｅｘ，ｆ′（ｘ）＝２ｘｅｘ＋ｘ２ｅｘ＝（ｘ２＋２ｘ）ｅｘ． 由ｆ′（ｘ）＞０，得ｘ２＋２ｘ＞０，ｘ＜－２或ｘ＞０；由ｆ′（ｘ）＜０，得ｘ２＋２ｘ ＜０，－２＜ｘ＜０．所以函数ｆ（ｘ）的单增区间是（－∞，－２］，［０，＋∞），单减区间是［－２，０］．　　

　　（２）ｆ（ｘ）＝ｘ２ｅａｘ，ｆ′（ｘ）＝２ｘｅａｘ＋ａｘ２ｅａｘ＝（ａｘ２＋２ｘ）ｅａｘ． 若函数ｆ（ｘ）＝在（－∞，－１］上递增，则在（－∞，－１］上ｆ′（ｘ）＝（ａｘ２＋２ｘ）ｅａｘ≥０，即ａｘ２＋２ｘ≥０．

　　因为ｘ∈（－∞，－１］，所以ｘ２＞０，ａｘ２＋２ｘ≥０变为ａ≥－2/x，ａ≥（－2/x）ｍａｘ． －2/x在ｘ∈（－∞，－１］上是减函数，最大值为－2/-1＝２，故ａ≥２， 即为实数ａ的取值范围． 

　　［点评］纵观近年来的高考题不难发现，“已知函数的单调性特征，反过来确定函数式中待定字母的取值范围”试题在高考中频频出现，而且试题的深度、广度和难度也在不断增大． 这种逆向设置的问题， 有一定的开发性，能有效考查学生对函数、导数、不等式思想方法的掌握程度、思维水平和综合能力． 显然， 这些试题用单调性的定义求解，将会十分复杂，甚至无法求解． 而运用导数符号与函数单调性的关系来处理则是一种有效途径． 对于可导函数ｆ（ｘ）在区间Ｄ上单增（或单减）的充要条件是：在ｘ∈Ｄ上恒有ｆ′（ｘ）≥０（或ｆ′（ｘ）≤０），且ｆ′（ｘ）在Ｄ的任意子区间上都不恒为零． 在高中阶段， 主要出现的是有一个或多个（有限个）使ｆ′（ｘ）＝０的点ｘ的情况． 比如， 函数ｆ（ｘ）＝ｘ３在（－∞，＋∞）上单增，ｆ′（ｘ）＝３ｘ２≥０在（－∞，＋∞）上恒成立， 其中有一个ｘ０＝０，使ｆ′（ｘ０）＝０成立． 注意ｆ′（ｘ）＞０（或ｆ′（ｘ）＜０）是ｆ（ｘ）为增（或减）函数的充分而非必要的条件， 避免当做充要条件使用． 这里不能由不等式ａｘ２＋２ｘ＞０求实数ａ的取值范围．

　　考点８． 分类讨论待定字母的取值范围问题

　　例８． 求函数ｆ（ｘ）＝ｘｌｎ（－ｘ）＋（ａ－１）ｘ（ａ∈Ｒ）在区间［－ｅ２，－ｅ－１］上的最大值ｇ（ａ）．

　　［解析］ｆ′（ｘ）＝ｌｎ（－ｘ）＋ ａ． 由ｆ′（ｘ）＝ｌｎ（－ｘ）＋ ａ＝０ ，得ｘ＝－ｅ－ａ．

　　①若－ｅ－ａ＜－ｅ２，即ａ＜－２，函数在［－ｅ２，－ｅ－１］上递减，ｇ（ａ）＝ｆ（－ｅ２） ＝－（ａ＋１）ｅ２．

　　②若－ｅ２≤－ｅ－ａ＜－ｅ－１，即－２≤ａ＜１时，ｇ（ａ）＝ｆ（－ｅ－ａ）＝ｅ－ａ．

　　③若－ｅ－ａ≥－ｅ－１，函数在［－ｅ２，－ｅ－１］上递增，ｇ（ａ）＝ｆ（－ｅ－１）＝■

　　［点评］本题中ａ为任意实数，ｆ′（ｘ）的零点ｘ＝－ｅ－ａ是否在所给的区间［－ｅ２，－ｅ－１］内，有ａ待于的取值，必须对零点ｘ＝－ｅ－ａ与区间［－ｅ２，－ｅ－１］的位置关系进行分类讨论． 一般地，分类讨论有“三步曲”：一是选择分类对像，即对什么东西进行分类（这里零点ｘ＝－ｅ－ａ与区间［－ｅ２，－ｅ－１］的位置关系由ａ确定，因此选择ａ为分类对像）；二是确定分类标准，即怎样分类（这里根据零点ｘ＝－ｅ－ａ在区间［－ｅ２，－ｅ－１］的左边、内部、右边分成ａ＜－２、－２≤ａ＜１和ａ≥１三类）；三是深化分类层次（就是在一级分类中再进行二级分类，即分类中分类，本题不涉及）． 导数、不等式在函数的应用中， 常常涉及到待定的字母，函数的单调性、极值、最值以及图像的形状等等都与字母的取值有关， 此时要牢记对待定字母的分类讨论， 切实把握分类讨论的“三步曲”，否则极易出错．

　　考点９． 函数的零点个数问题

　　例９． 试判断函数ｆ（ｘ）＝ｘ２－８ｌｎｘ－８的零点个数．

　　［解析］函数ｆ（ｘ）的定义域是（０，＋∞）． 由ｆ′（ｘ）＝２ｘ－8/x＝０，得ｘ＝±２，取ｘ＝２．

　　当０＜ｘ＜２时，ｆ′（ｘ）＜０；当ｘ＞２时，ｆ′（ｘ）＞０ ．所以函数ｆ（ｘ）在点ｘ＝２处取极小值，也是最小值， 且最小值为ｆ（２）＝２２－８ｌｎ２－８＝－４－８ｌｎ２＜０．

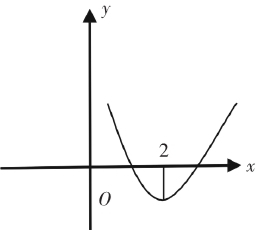
　　如图３，当ｘ逐渐靠近零时，ｆ（ｘ）越来越大；当ｘ大于２，并逐渐大时，ｆ（ｘ）也越来越大．因此函数ｆ（ｘ）有两个零点．

　　［点评］超越函数的零点个数用传统方法处理往往不易，导数是很好的工具．解题的基本步骤是：求ｆ′（ｘ）＝０的根ｘ０；判断在根ｘ０的两侧ｆ′（ｘ）的符号；确定ｘ０是极大值点，还是极小值点，或不是极值点；求最值；画出ｆ（ｘ）的草图，观察即可．

　　考点１０． 函数图像的交点个数问题 

　　例１０． 已知ｆ（ｘ）＝－ｘ２＋８ｘ，ｇ（ｘ）＝６ｌｎｘ＋ｍ，是否存在实数ｍ，使得函数ｙ＝ｆ（ｘ）的图像与函数ｙ＝ｇ（ｘ）的图像有且只有一个交点？若存在，请求出ｍ的取值范围； 若不存在，请说明理由．

　　［解析］函数的ｙ＝ｆ（ｘ）图像与函数ｙ＝ｇ（ｘ）的图像的交点个数问题，就是方程ｆ（ｘ）＝ｇ（ｘ）在（０，＋∞）上实根的个数问题，进一步就是函数ｈ（ｘ）＝ｇ（ｘ）－ｆ（ｘ） 的图像与ｘ轴交点的个数问题．

　　因为ｈ（ｘ）＝６ｌｎｘ＋ｍ＋ｘ２－８ｘ，所以（ｘ＞０），

　　当０＜ｘ＜１时，ｈ′（ｘ）＞０，ｈ（ｘ）单调递增； 当１＜ｘ＜３时，ｈ′（ｘ）＜０，ｈ（ｘ）单调递减； 当ｘ＞３时ｈ′（ｘ）＞０，ｈ（ｘ）单调递增． 所以ｈ（ｘ）的极大值为ｈ（１）＝ｍ－７，极小值为ｈ（３）＝ｍ＋６ｌｎ３－１５，并且当ｘ→＋∞时，ｈ（ｘ）→＋∞；当ｘ→０＋时， ｈ（ｘ）→－∞． 因此要使ｈ（ｘ）＝ｇ（ｘ）－ｆ（ｘ）＜０的图像与ｘ轴有且只有一个交点，必须且只（下转第２３页）