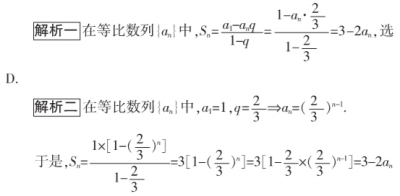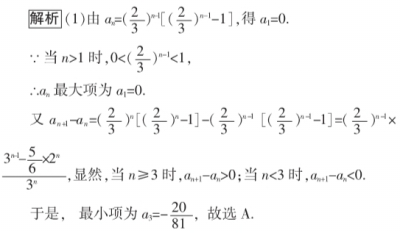纵观近三年广东高考数学试卷，无论文科还是理科，对于数列内容的考查相对比较稳定，试题一大一小，分数为１９分．试题内容也比较相似，小题都是考查等差、等比数列的通项公式与前ｎ项和公式的应用，此题的难度很小，百分之八十以上的考生都能顺利得分．大题都与递推关系或通项ａｎ与前ｎ项和Ｓｎ的关系有关，然后考查求具体的项与通项公式，最后都是与不等式有关的证明问题，且在证明过程中又都无一例外的用到裂项与放缩技巧．２０１４年呢？由于高考命题要求在稳定中创新、在中改革，于是，我们预测其命题热点有以下几个方面，供参考．

　　热点一：客观题仍考查等差、等比数列的基础知识与简单的常用技能

　　例１． 设首项为１，公比为2/3的等比数列｛ａｎ｝的前ｎ项和为Ｓｎ，则（　　）

　　Ａ． Ｓｎ＝２ａｎ－１　　　　　　　　Ｂ． Ｓｎ＝３ａｎ－２

　　Ｃ． Ｓｎ＝４－３ａｎ　　　　　　　　Ｄ． Ｓｎ＝３－２ａｎ

　　点评 等差、等比数列的基础知识与简单的常用技能是处理数列问题的思维起点，也是数列中应用数学思想方法的入手点，因此，在各级各类的考试中对这些内容的考查作为检查高中生对基础知识的普遍掌握情况十分有利．

　　热点二：客观题转变考查方向，建立在数列基础知识与基本技能的基础上考查分析与推理能力

　　例２． 已知数列｛ａｎ｝的通项为ａｎ＝（2/3）ｎ－１［（2/3）ｎ－１－１］，下列表述正确的是（　　）

　　Ａ． 最大项为０，最小项为－20/81

　　Ｂ． 最大项为０，最小项不存在

　　Ｃ． 最大项不存在，最小项为－20/81

　　Ｄ． 最大项为０，最小项为ａ４

　　点评 从函数角度来认识本题最有利于求解，函数的最值往往与单调性有关，那么数列的最值呢？也与数列的单调性有关，于是，借助数列的单调性最终产生结论．

　　例３． 数列｛ａｎ｝满足ａｎ＋１＋（－１）ｎａｎ＝２ｎ－１，则｛ａｎ｝的前６０项和为＿＿＿＿＿＿＿．

　　解析一 由题设知，ａ２－ａ１＝１…①；ａ３＋ａ２＝３…②；ａ４－ａ３＝５…③；ａ５＋ａ４＝７…④；ａ５＋ａ４＝７，ａ６－ａ５＝９，ａ７＋ａ６＝１１，ａ８－ａ７＝１３，ａ９＋ａ８＝１５，ａ１０－ａ９＝１７，ａ１１＋ａ１０＝１９，ａ１２－ａ１１＝２１，．．．．．．

　　∴②－①得ａ１＋ａ３＝２，③＋②得ａ４＋ａ２＝８，

　　同理可得ａ５＋ａ７＝２，ａ６＋ａ８＝２４，ａ９＋ａ１１＝２，ａ１０＋ａ１２＝４０，…，

　　∴ａ１＋ａ３，ａ５＋ａ７，ａ９＋ａ１１，…，是各项均为２的常数列，

　　ａ２＋ａ４，ａ６＋ａ８，ａ１０＋ａ１２，…是首项为８，公差为１６的等差数列，

　　则｛ａｎ｝的前６０项和为１８３０．

　　点评 本题无论是方法一还是方法二，在规定的时间内都不太好想，说它很难吧，不是；说它不难吧，显然也不准确．反复应用递推关系是求解的关键．

　　热点三：解答题延续去年的热点，继续建立在ａｎ与ｓｎ关系的基础上考查通项公式的求法及放缩法证明不等式

　　例４． 数列｛ａｎ｝的前ｎ项和为Ｓｎ，已知ａ１＝1/2，Ｓｎ＝ｎ２ａｎ－ｎ（ｎ－１），ｎ＝１，２，…