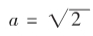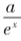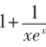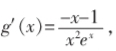作为一种数学思想方法，数形结合的应用大致又可分为两种情形：或者借助于数的精确性来阐明形的某些属性，或者借助形的几何直观性来阐明数之间某种关系，即数形结合包括两个方面：第一种情形是“以数解形”，而第二种情形是“以形助数”．“以数解形”就是有些图形太过于简单，直接观察却看不出什么规律来，这时就需要给图形赋值，如边长、角度等等，特别是在做选择题时，只有一个答案是正确答案，用此种方法就可能起到意想不到的效果．“以形助数”是指把抽象的数学语言转化为直观的图形，可避免繁杂的计算，获得出奇制胜的解法．“以形助数”中的“形”，或有形或无形．若有形，则可为图表与模型，若无形，则可另行构造或联想．因此“以形辅数”的途径大体有三种：一是运用图形；二是构造图形；三是借助于代数式的几何意义．但由于构造图形的误差，或者“无中生有”的不准确，有时可能会出现一些错误．本文就运用数形结合时容易出现的失误做个简单的归类分析，希望引起你的重视．

　　１． 潦草作图而导出的错误

　　在同一坐标系中作几个函数的图像来比较时，我们一定要注意函数图像的延伸趋势以及伸展“速度”．因为我们画出的只是函数图像的一小部分，而不是全部．常言到“知人知面不知心”，同样的，我们从函数图像的部分而知道它的全部，在没画出来的部分图像是怎么样的呢？我们只有根据函数图像的延伸趋势以及伸展“速度”来判断了．

　　例１． 判断命题“当ａ＞１时，关于ｘ的方程ａｘ＝ｌｏｇ ａ ｘ无实数解”是否正确？

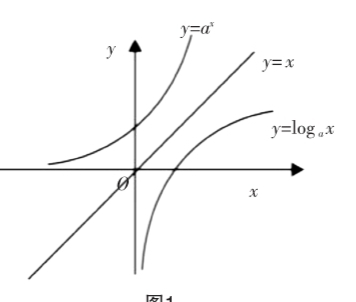
　　错解：在同一坐标系中，分别画出函数 ｙ＝ａｘ（ａ＞１）及ｙ＝ｌｏｇ ａ ｘ（ａ＞１）的图像，如图１所示，可见它们没有公共点，所以方程确无实数解，故命题正确．

　　剖析：实际上对不同的实数ａ，ｙ＝ａｘ及ｙ＝ｌｏｇ ａ ｘ的图像的延伸趋势不同，例如当ａ ＝ ２时，原方程无实数解；而当时 ，ｘ ＝ ２ 便是原方程的解．上面的错解就是潦草作图，而画出了个有误差的图形，并且想当然地根据图形而不去注意函数图像的延伸趋势而造成的．

　　事实上，我们还可以通过几何画板的演示（参数ａ可动态控制），在同一坐标系中作出函数ｙ＝ａｘ和函数ｙ＝ｌｏｇ ａ ｘ（ａ＞０，ａ≠１）的图像，当ａ非常小时它们有三个交点，此时，方程ａｘ＝ｌｏｇ ａ ｘ解的有３个．

　　例２． 比较２ｎ与 ｎ２（ｎ 大于１的自然数）的大小．

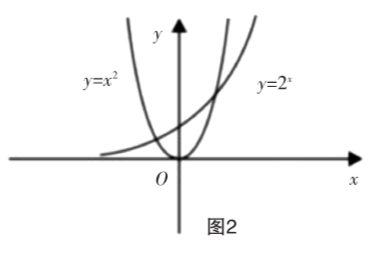
　　错解：在同一坐标系中分别画出函数ｙ＝２ｘ及ｙ＝ｘ２的图像，如图２所示，由图可知，两个图像有一个公共点．当ｘ＝２时，２ｘ＝ｘ２，当ｘ ＞ ２时有２ｘ＜ｘ２成立，所以，当ｎ＝２时 ２ｎ＝ｎ２，而且当ｎ 是大于２的自然数时，２ｎ＜ｎ２．

　　剖析：事实上，当ｎ＝ ４时，２ｎ与 ｎ２，也相等；ｎ＝ ５时，２ｎ＞ｎ２．错解是因为没有充分注意到两图像的递增“速度”！要比较两个图像的递增速度，确实很难由图像直观而得．本题可以先猜想，后用数学归纳法证明．本题的正确答案是　当ｎ＝２，４时２ｎ＝ｎ２，当ｎ＝３时 ，２ｎ＜ｎ２，当ｎ是大于４的自然数时，２ｎ＞ｎ２，证明略．

　　例３．（２０１３年高考·福建卷，文２２题改编）已知函数ｆ（ｘ）＝ｘ－１＋（ａ∈Ｒ，ｅ为自然对数的底数）．当ａ＝１时，若直线ｌ：ｙ＝ｋｘ－１与曲线ｙ＝ｆ（ｘ）没有公共点，求ｋ的最大值．

　　解析：由题意，方程ｋｘ－１＝ｘ－１＋无解，显然ｘ＝０不是方程的解，故分离参数后的方程ｋ＝１＋无解．令ｇ（ｘ）＝（ｘ≠０），则，所以ｇ（ｘ）在（－∞，－１）上单调递增，在（－１，０）和（０，＋∞）上单调递减，在ｘ＝－１处取到极大值ｇ（－１）＝１－ｅ．又当ｘ→０＋时，ｇ（ｘ）→＋∞；当ｘ→０－时，ｇ（ｘ）→－∞；当ｘ→＋∞时，ｇ（ｘ）→１；当ｘ→－∞时，ｇ（ｘ）→－∞，即直线ｘ＝０和ｙ＝１是函数ｇ（ｘ）的两条渐近线，所以ｇ（ｘ）的大致图像如图３．由题意知，直线ｙ＝ｋ与函数ｇ