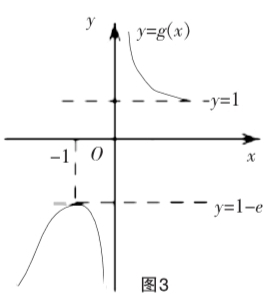
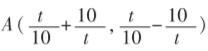点评：本题为含参函数的零点问题，解决这类问题的常用方法是分离参数之后转化为等式两边的函数图像是否有交点问题，因此准确的作图至关重要．但考生在用导数法研究函数图像的变化趋势时，通常只关注函数的单调性与极值，而对函数图像是否存在渐近线意识淡薄，因而常常造成作图错误．本题中函数ｇ（ｘ）在ｘ＝０处没有定义，考生通常仅将此点在函数图像上“挖空”，表示函数图像在此处“中断”，而不会意识到ｘ＝０是函数图像的渐近线．这是缺乏极限意识的表现．因此，要纠正上述错误，须树立极限意识，即在探明函数单调性之后，还要对单调区间两端的“断点”处分别求极限，以了解函数图像的走势与范围，如此方可给图像以相对准确的定位，避免作图的随意性．

　　２． 定义域扩大或缩小引起的错误

　　例４． 设ｔ＞０，求点与点Ｂ（－１， ０）之间距离的最小值．

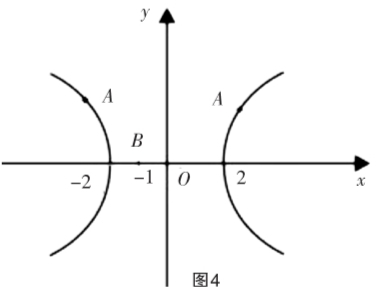
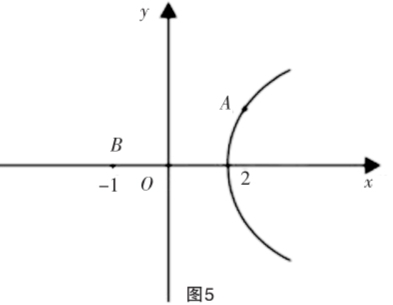
　　解析：由点可知点Ａ的轨迹为ｘ２－ｙ２＝４，如图４所示，可知｜ＡＢ｜的最小值为１．其实这是错误的，原因就是忽视了变的量取值范围，由ｔ＞０知ｘ≥２，正确的图像应该是图５的右图，可知其最小值为３．

　　点评：定义域是一个变量的最大范围，如果不注意转化过程是否是等价的过程，那么变量的定义域就有可能扩大或缩小了，这样，画出来的图像就会多出一部分或者少了一角，而根据这样有误差的图像，做出来的结果是会不准确的，那就是白做了这道题，所以注意转化过程要等价是关键的．不论是否注意到转化过程要等价，我们最好能做好一道题，就再用另外一种方法验证一下所得到的答案是否准确，这样才会有信心地保证做完一题就一定正确．