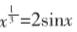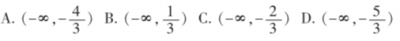错解：∵点Ａ在曲线ｆ（ｘ）＝－ｘ２＋３ｘ上，且ｆ′（ｘ）＝－３ｘ２＋３，∴ ｆ（２）＝－９．

　　故所求切线方程为ｙ＋２＝－９（ｘ－２），即９ｘ＋ｙ－１６＝０．

　　正解：设切点为Ｐ（ｘ０，ｙ０），

　　∵ｆ′（ｘ）＝－３ｘ２＋３，

　　∴在点Ｐ处的切线方程为ｙ－ｙ０＝（３－３ｘ０２）（ｘ－ｘ０）．

　　又切线过点Ａ，

　　∴ －２－（３ｘ０－ｘ０３）＝（３－３ｘ０２）（２－ｘ０），

　　整理得ｘ０３－３ｘ０２＋４＝０，即（ｘ０＋１）（ｘ０－２）２＝０，

　　∴ｘ０＝－１或ｘ０＝２．

　　当ｘ０＝－１时，切线经过点Ｐ（－１，－２）和Ａ（２，－２），切线方程为ｙ＝－２；当ｘ０＝２时，切线方程为９ｘ＋ｙ－１６＝０．

　　剖析：本题遗漏了ｙ＝２这条切线，失误的原因是把过点Ａ的切线理解成在点Ａ处曲线的切线．曲线在点Ａ处的切线指的是切点在点Ａ处的切线，而过点Ａ的切线除了切点在点Ａ处的曲线切线还可能存在切点不在点Ａ处而经过点Ａ的切线，两者是有区别的．因此，解题时必须理清头绪，分清这两个易混淆的概念．其实，“曲线在某点处的切线”不是“过曲线上某点的切线”充分必要条件，而是必要不充分条件．

　　５． 证明问题时逻辑循环引起的错误

　　“形”并不能作为证明的依据，遇到证明题时，在几何直观分析的同时，还要进行代数抽象的探索，并用严谨的数学语言写出证明过程的理论依据，这样才算做好证明题．应用数形结合时，“形”只是一种手段，一个工具，而不是理论依据．不论是怎么样的题目，“形”只是我们思考问题的种方式，为解题提供一些帮助，但我们都要写出我们做这道题的理论依据，这样才会让人知道你不是直接从图像中看出来的或者是猜测得到的，这样才有说服力，有是有效的．

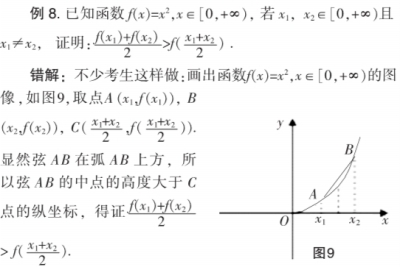
　　剖析：这里要证明的不等式，正是凹函数的定义，用凹函数的直观图形来证明不等式成立是一个逻辑循环，自己来证明自己．其实，用作差法即可证明．本题的定义域可改为全体实数也成立．

　　总之，数形结合的确是一个非常好，也非常实用而且重要的思想方法，应用性强．但它又是一把双刃剑，有诱惑也有陷阱．因此，我们在运用时，要注意利用“数”的精确性，注意数形转化的等价性，注意图形的全面性，在直观的同时，辅有严谨的演绎．

　　你来做做：

　　２． 方程＝２ｓｉｎｘ的解的个数是（　　  ）

　　Ａ． ６个　　　　Ｂ． ７个　　　　Ｃ． ８个　　　　Ｄ． ９个

　　３．（２０１３北京卷，理科８）设关于ｘ，ｙ的不等式组２ｘ－ｙ＋１＞０，ｘ＋ｍ＜０，ｙ－ｍ＞０表示的平面区域内存在点Ｐ（ｘ０，ｙ０）满足ｘ０－２ｙ０＝２，求得ｍ的取值范围是（　　  ）

　　４． 当ｘ∈（１，２）时不等式（ｘ－１）２＜ｌｏｇａ ｘ恒成立，则实数ａ的取值范围是（ ）