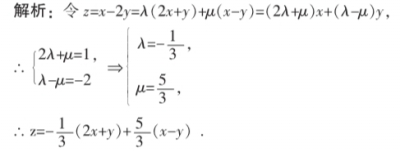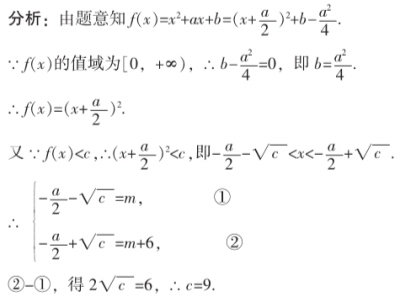一、复习指南

　　１． 在复习中要注意扎扎实实地掌握基础知识和基本方法，特别是要掌握不等式的性质和等价转化的原则，它是学好本章内容的关键，证明不等式没有固定的模式可套，它方法灵活，技巧性强，因此在复习中除掌握比较法、分析法、综合法这三种基本方法外，还应了解其它的证明方法，并不断总结证明不等式的规律和技巧，提高数学能力．

　　２． 强化本章常用的数学思想方法的复习．①等价转化的思想：如在不等式的同解变形过程中等价转化思想起重要作用，解不等式的过程实质上就是利用不等式的性质进行等价转化的过程．②分类讨论的思想：如求解含参数的不等式问题，一般要对参数进行分类讨论，在复习时，应学会分析引起分类讨论的原因，合理地分类，做到不重不漏．③函数与方程思想：不等式与函数、方程三者相互联系、相互转化，如求参数的取值范围问题，函数与方程的思想是解决这类问题的重要方法．④化归思想：证明不等式就是将已知条件转化为要证的结论，这体现了化归思想的重要性，其中不仅考查基础知识，而且能考查出考生分析问题和解决问题的能力．

　　３． 在复习时应强化不等式的应用，提高应用意识．历届高考题中除单独考查不等式的试题外，常在一些函数、数列、立体几何、解析几何和实际应用的问题中涉及不等式，如在实际问题中，主要有构造不等式求解或构造函数求最值，求最值时要注意等号成立的条件．因此，在复习过程中，一定要提高应用意识，不断总结不等式的应用规律，努力提高数学能力．

　　二、典题选析

　　题型１． 利用不等式性质求取值范围．

　　例１． 若变量ｘ，ｙ满足约束条件３≤２ｘ＋ｙ≤９，６≤ｘ－ｙ≤９，则ｚ＝ｘ－２ｙ的最小值为＿＿＿＿＿＿＿＿＿＿．

　　分析：利用不等式性质求某些代数式的取值范围时，应注意两点：一是必须严格运用不等式的性质；二是在多次运用不等式的性质时有可能扩大了变量的取值范围，要特别注意．

　　又∵ ３≤２ｘ＋ｙ≤９，６≤ｘ－ｙ≤９，

　　∴７≤－1/3（２ｘ＋ｙ）＋5/3（ｘ－ｙ）≤１４，即７≤ｚ≤１４，

　　∴ ｚｍｉｎ＝７．

　　点评：本题也可用线性规划求解，但题中ｘ，ｙ相互制约，不可分割，先待定系数法建立待求范围的整体与已知范围的整体的等量关系，最后通过“一次性”不等关系的运算求得待求整体的范围是避免错误的一条途径．

　　题型２． 三个“二次”间的关系

　　例２． 已知函数ｆ（ｘ）＝ｘ２＋ａｘ＋ｂ（ａ，ｂ∈Ｒ）的值域为［０，＋∞），若关于ｘ的不等式ｆ（ｘ）＜ｃ的解集为（ｍ，ｍ＋６），则实数ｃ的值为＿＿＿＿＿＿＿＿＿＿．

　　点评：二次函数、一元二次不等式、一元二次方程之间有着密切关系．（１）一元二次不等式解集的端点就是对应的一元二次方程的解；（２）不等式的解集结构与二次项系数有直接的关系；（３）二次函数的图像能直观反映一元二次不等式解集的情况．