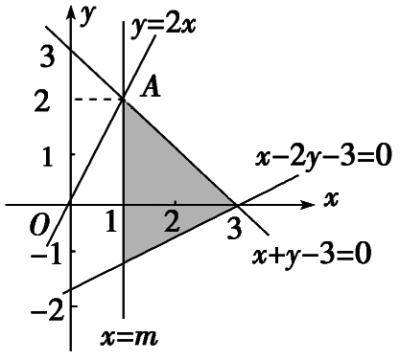
例４． 若直线ｙ＝２ｘ上存在点（ｘ，ｙ）满足约束条件ｘ＋ｙ－３≤０，ｘ－２ｙ－３≤０，ｘ≥ｍ，则实数ｍ的最大值为（　　）

　　Ａ． －１　　　　   Ｂ． １　　　　   Ｃ．3/2　　　　   Ｄ． ２

　　分析：（１）利用条件作出直线ｙ＝２ｘ，ｘ＋ｙ－３＝０，ｘ－２ｙ－３＝０．（２）由图形知，当直线ｘ＝ｍ过点Ａ（１，２）（即直线ｙ＝２ｘ和ｘ＋ｙ－３＝０的交点）时满足条件．

　　解析：　

　　首先作出约束条件ｘ＋ｙ－３≤０，ｘ－２ｙ－３≤０，ｘ≥ｍ对应的可行域及直线ｙ＝２ｘ，

　　如图，易知直线ｘ＝ｍ过点Ａ（１，２）时符合题意，即此时

　　ｘ＝ｍ＝１为ｍ的最大值．

　　点评：解决含参数的线性规划问题时应掌握：（１）解题时要看清题目，不能忽视或漏掉参数的范围；（２）对于题目中最值条件的确定至关重要，且不能计算出错．

　　题型５． 利用基本不等式解决实际问题

　　对于应用题要通过阅读，理解所给定的材料，寻找量与量之间的内在联系，抽象出事物系统的主要特征与关系，建立起能反映其本质属性的数学结构，从而建立起数学模型，然后利用不等式的知识求出题中的问题。

　　例５． 某食品厂定期购买面粉，已知该厂每天需要面粉６吨，每吨面粉的价格为１ ８００元，面粉的保管等其他费用为平均每吨每天３元，购买面粉每次需支付运费９００元．

　　（１）求该厂多少天购买一次面粉，才能使平均每天所支付的总费用最少？

　　（２）若提供面粉的公司规定：当一次购买面粉不少于２１０吨时，其价格可享受９折优惠（即原价的９０％），问该厂是否考虑利用此优惠条件？请说明理由．

　　分析：（１）利用基本不等式解决实际问题时，应先仔细阅读题目信息，理解题意，明确其中的数量关系，并引入变量，依题意列出相应的函数关系式，然后用基本不等式求解．

　　（２）求所列函数的最值，若用基本不等式时，等号取不到，可利用函数单调性求解．

　　解析：（１）设该厂应每隔ｘ天购买一次面粉，其购买量为６ｘ吨．由题意知，面粉的保管等其他费用为３［６ｘ＋６（ｘ－１）＋…＋６×２＋６×１］＝９ｘ（ｘ＋１）．

　　∴当ｘ＝３５时，ｆ（ｘ）有最小值，此时ｙ２＜１０ ９８９，

　　∴该厂应接受此优惠条件．

　　点评：利用基本不等式求最值时，一定要注意应用基本不等式成立的条件：即一正，二定，三相等，否则求解时会出现等号成立的条件不具备而出错．若在同一题目中，两次或两次以上利用基本不等式，等号应同时成立．

　　题型６． 绝对值三角不等式性质定理的应用

　　例６．“｜ｘ－ａ｜＜ｍ，且｜ｙ－ａ｜＜ｍ”是“｜ｘ－ｙ｜＜２ｍ”（ｘ，ｙ，ａ，ｍ∈Ｒ）的（　　  ）

　　Ａ． 充分非必要条件　　　　　　 Ｂ． 必要非充分条件　　

　　Ｃ． 充要条件　　　　　　　　　　  Ｄ． 非充分非必要条件

　　分析：利用绝对值三角不等式，推证｜ｘ－ａ｜＜ｍ，且｜ｙ－ａ｜＜ｍ与｜ｘ－ｙ｜＜２ｍ的关系即得答案．

　　解析：选Ａ．

　　∵ ｜ｘ－ｙ｜＝｜（ｘ－ａ）－（ｙ－ａ）｜≤｜ｘ－ａ｜＋｜ｙ－ａ｜＜ｍ＋ｍ＝２ｍ．

　　∴ ｜ｘ－ａ｜＜ｍ，且｜ｙ－ａ｜＜ｍ是｜ｘ－ｙ｜＜２ｍ的充分条件．

　　取ｘ＝３，ｙ＝１，ａ＝－２，ｍ＝２．５，则有｜ｘ－ｙ｜＝２＜５＝２ｍ，但｜ｘ－ａ｜＝５，不满足｜ｘ－ａ｜＜ｍ＝２．５，

　　故｜ｘ－ａ｜＜ｍ且｜ｙ－ａ｜＜ｍ不是｜ｘ－ｙ｜＜２ｍ的必要条件．

　　点评：（１）对绝对值三角不等式定理｜ａ｜－｜ｂ｜≤｜ａ±ｂ｜ ≤｜ａ｜＋｜ｂ｜中等号成立的条件要深刻理解，特别是用此定理求函数的最值时．