(3)对于求y=|x-a|+|x-b|或y=|x+a|-|x-b|型的最值问题利用绝对值三角不等式更简捷、方便.
题型7. 绝对值不等式的解法
例7. 解下列不等式:
(1)1<|x-2|≤3;
(2)|2x+5|>7+x;
(3)|x2-9|≤x+3;
(4)|x-1|+|x-2|<5.
分析:(1)利用公式或平方法转化为不含绝对值的不等式;(2)利用公式法转化为不含绝对值的不等式; (3)利用绝对值的定义或|f(x)|≤a(a>0)?圯-a≤|f(x)|≤a去掉绝对值符号或利用数形结合思想求解; (4)不等式的左边含有绝对值符号,要同时去掉这两个绝对值符号,可以采用“零点分段法”,此题亦可利用绝对值的几何意义去解.
解析:(1)原不等式等价于不等式组|x-2|>1,x-2≤3,即x<1或x>3,-1≤x≤5,
解得-1≤x<1或3<x≤5,
所以原不等式的解集为{x|-1≤x<1或3<x≤5}.
(2)由不等式|2x+5|>7+x,
可得2x+5≥0,2x+5>7+x或 2x+5<0,2x+5<-(7+x),解得x>2或x<-4.
∴原不等式的解集是{x| x<-4或x>2}
(3)原不等式?圳① x2-9≥0,x2-9≤x+3或② x2-9<0,9-x2-≤x+3,
不等式①?圳x≤-3或x≥3,-3≤x≤4?圳 x=-3或3≤x≤4.
不等式②?圳-3<x<4,x≤-3或x≥2?圳2≤x<3.
∴原不等式的解集是{x|2≤x≤4或x=-3}.
(4)分别求|x-1|,|x+2|的零点,即1,-2.由-2,1把数轴分成三部分:x<-2,-2≤x≤1,x>1.
当x<-2时,原不等式即1-x-2-x<5,解得-3<x<-2;
当-2≤x≤1时,原不等式即1-x+2+x<5,因为3<5恒成立,则-2≤x≤1;
当x>1时,原不等式即x-1+2+x<5,解得1<x<2.
综上,原不等式的解集为{x|-3<x<2}.
点评:(1)形如|x-a|±|x-b|≥c不等式的解法常用零点分段讨论法,其步骤为:①求零点;②划分区间、去绝对值号;③分别解去掉绝对值的不等式;④取每个结果的并集,特别注意在分段时不要漏掉区间的端点值.(2)上述不等式也可用|x-a1|±|x-a2|的几何意义去求解集.
题型8. 含参数的绝对值不等式
例8. 若关于x的不等式|x+2|+|x-1|≤a的解集为?椎,求实数a的取值范围.
分析:把不等式问题转化为函数的图像,利用数形结合思想求解;也可以运用绝对值的几何意义求解.
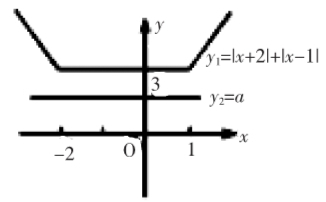
解析:令y1=|x+2|+|x-1|,y2=a,∴ y1=2x+1, (x≥1)3, (-2≤x<1)-2x-1. (x<-2)
y1、y2的图像如图所示.
由图可知,当a<3时,|x+2|+|x-1|≤a的解集为?椎.
题型9. 绝对值不等式的综合问题
例9. 已知a、b、c是实数,函数f(x)=ax2+bx+c,g(x)=ax+b,当-1≤x≤1时,|f(x)|≤1.
(1)证明:|c|≤1;
(2)证明:当-1≤x≤1时,|g(x)|≤2;
(3)设a>0,当-1≤x≤1时,g(x)的最大值是2,求f(x).
分析:(1)代入x=0即得;(2)结合一次函数的单调性和绝对值不等式的性质得证;(3)结合二次函数的图像和一次函数的最值求解.
解析:(1)由已知,当-1≤x≤1时,|f(x)|≤1,取x=0,得|c|=|f(0)|≤1,即|c|≤1.
(2)当a>0时,g(x)=ax+b在[-1,1]上是增函数,所以g(-1)≤g(x)≤g(1),
因为|f(x)|≤1(-1≤x≤1),|c|≤1,所以g(1)=a+b=f(1)-c≤
|f(1)|+|c|≤2.
g(1)=-a+b=-f(-1)+c≥-(|f(-1)|+|c|)≥-2.
由此可得|g(x)|≤2;
当a<0时,g(x)=ax+b在[-1,1]上是减函数,所以g(-1)≥g(x)≥g(1),
因为|f(x)|≤1(-1≤x≤1),|c|≤1,所以g(-1)=-a+b=-f(-1)+c≤f(-1)+|c|≤2.
g(1)=a+b=f(1)-c≥-(|f(1)|+|c|)≥-2.由此得|g(x)|≤2;
当a=0时,g(x)=b,f(x)=bx+c,因为-1≤x≤1.
所以g(x)=|f(1)-c|≤|f(1)|+|c|≤2.
综上,得g(x)≤2.
(3)因为a>0,g(x)在[-1,1]上是增函数,当x=1时取得最大值2.
即g(1)=a+b=f(1)-f(0)=2,
因为-1≤f(0)=f(1)-2≤1-2=-1,所以c=f(0)=-1.
因为当-1≤x≤1时,f(x)≥-1,即f(x)≥f(0).
根据二次函数性质,直线x=0为二次函数f(x)的图象的对称轴.
所以-b/2a=0,即b=0,a=2,
故有f(x)=2x2-1.