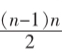热点八：解答题建立在新定义的基础上考查创新知识的应用

　　例９． 如果由数列｛ａｎ｝生成的数列｛ｂｎ｝满足对任意的ｎ∈Ｎ?鄢均有ｂｎ＋１＜ｂｎ，其中ｂｎ＝ａｎ＋１－ａｎ，则称数列｛ａｎ｝为“Ｚ数列”．

　　（Ⅰ）在数列｛ａｎ｝中，已知ａｎ＝－ｎ２，试判断数列｛ａｎ｝是否为“Ｚ数列”；

　　（Ⅱ）若数列｛ａｎ｝是“Ｚ数列”，ａ１＝０，ｂｎ＝－ｎ，求ａｎ；

　　（Ⅲ）若数列｛ａｎ｝是“Ｚ数列”，设ｓ，ｔ，ｍ∈Ｎ?鄢，且ｓ＜ｔ，求证：ａｔ＋ｍ－ａｓ＋ｍ＜ａｔ－ａｓ．

　　解析 （Ⅰ）因为ａｎ＝－ｎ２，所以ｂｎ＝ａｎ＋１－ａｎ＝－（ｎ＋１）２＋ｎ２＝－２ｎ－１，ｎ∈Ｎ?鄢， 

　　所以ｂｎ＋１－ｂｎ＝－２（ｎ＋１）－１＋２ｎ＋１＝－２，

　　所以ｂｎ＋１＜ｂｎ，数列｛ａｎ｝是“Ｚ数列”．

　　（Ⅱ）因为ｂｎ＝－ｎ，

　　所以ａ２－ａ１＝ｂ１＝－１，ａ３－ａ２＝ｂ２＝－２，…，ａｎ－ａｎ－１＝ｂｎ－１＝－（ｎ－１），

　　所以ａｎ－ａ１＝－１－２－…－（ｎ－１）＝－■（ｎ≥２），所以ａｎ＝－■（ｎ≥２），又ａ１＝０，所以ａｎ＝－■（ｎ∈Ｎ?鄢）．

　　（Ⅲ）因为ａｓ＋ｍ－ａｓ＝（ａｓ＋ｍ－ａｓ＋ｍ－１）＋…＋（ａｓ＋１－ａｓ）＝ｂｓ＋ｍ－１＋…＋ｂｓ，

　　ａｔ＋ｍ－ａｔ＝（ａｔ＋ｍ－ａｔ＋ｍ－１）＋…＋（ａｔ＋１－ａｔ）＝ｂｔ＋ｍ－１＋…＋ｂｔ，

　　又ｓ，ｔ，ｍ∈Ｎ?鄢，且ｓ＜ｔ，所以ｓ＋ｉ＜ｔ＋ｉ，ｂｓ＋ｉ＞ｂｔ＋ｉ，ｎ∈Ｎ?鄢，

　　所以ｂｓ＋ｍ－１＞ｂｔ＋ｍ－１，ｂｓ＋ｍ－２＞ｂｔ＋ｍ－２，…，ｂｓ＞ｂｔ，

　　所以ａｔ＋ｍ－ａｔ＜ａｓ＋ｍ－ａｓ，即ａｔ＋ｍ－ａｓ＋ｍ＜ａｔ－ａｓ．

　　关于数列的命题我们就谈这么多，真正的试题到底是什么样的题呢？我们期待与这里说的热点一致．

　　（作者单位：中山一中）

　　责任编校   徐国坚