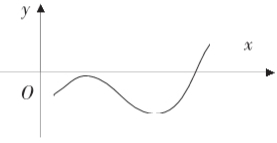
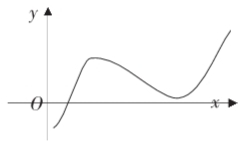
须ｈ（１）＝ｍ－７＜０（图４）或ｈ（３）＝ｍ＋６ｌｎ３－１５＞０（图５），即ｍ＜７或ｍ＞１５－６ｌｎ３时， 函数ｙ＝ｆ（ｘ）的图像与函数ｙ＝ｇ（ｘ）的图像有且只有一个交点．

　　变式１：如果“函数ｙ＝ｆ（ｘ）的图像与函数ｙ＝ｇ（ｘ）的图像有且只有一个交点”变为“函数ｙ＝ｆ（ｘ）的图像与函数ｙ＝ｇ（ｘ）的图像有且只有两个不同交点”，怎样解答呢？

　　变式２：如果“函数ｙ＝ｆ（ｘ）的图像与函数ｙ＝ｇ（ｘ）的图像有且只有一个交点”变为“函数ｙ＝ｆ（ｘ）的图像与函数ｙ＝ｇ（ｘ）的图像有且只有三个不同交点”，怎样解答呢？

　　［点评］用导数探讨函数ｙ＝ｆ（ｘ）的图像与函数ｙ＝ｇ（ｘ）的图像的交点个数问题，也是近年来高考考查的热点内容之一． 解题的主要步骤是：①构造函数ｈ（ｘ）＝ｇ（ｘ）－ｆ（ｘ）；②求导ｈ′（ｘ）＝ｇ′（ｘ）－ｆ′（ｘ）；③研究函数ｈ（ｘ）的单调性和极值（必要时研究函数图像端点的极限情况）；④画出函数ｈ（ｘ）的草图，观察与ｘ轴的交点情况，列出相应的不等式（组）；⑤解不等式（组）获解．

　　以上对函数、导数、不等式在２０１４年高考中的考点作了十个方面的预测． 这些试题很好地体现了函数、导数与不等式的联系，以及解函数、导数与不等式问题的核心思想方法，有一定的价值．高考题无非是知识与思想方法的重新排列组合，尽管我们无法猜到原题，但万变不离其宗，熟练把握了这十种题型，可以在高考中以不变应万变． 

　　（作者单位：安徽省太湖中学）

　　责任编校 徐国坚