教学片段：

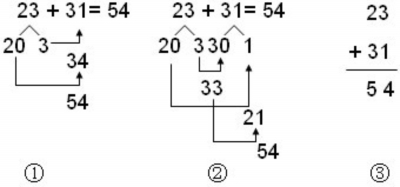
　　新课导入，教师揭示课题后，让学生独自口算２３＋３１，并写出口算的过程。同时，教师巡堂收集学生具有代表性的思维样本并板书，具体如下：

　　由于本课的教学是基于学生的生成资源而展开的，而学生的资源生成也必然会意想不到，对于③的出现，尽管它脱离了本课的教学要求，但其计算原理与本课口算方法存在着本质上的相同性，有助于学生全面把握口算的内在关联与本质，鉴于它独特的教学价值，我把③保留下来作为下一步教学资源。

　　师：同学们，老师收集了一些同学们的口算方法，你们能看懂他们是怎么算的吗？同桌说说看。

　　学生互说黑板上的不同的口算方法。

　　师：同学们，我们先来看①和②的口算方法，从它们的计算过程上来看，有什么相同和不同的地方？我们先说相同的。

　　生１：两种方法都把２３分拆成２０和３。

　　生２∶３１也被分拆成３０和１。

　　师：也就是说，他们都对加数进行了分拆，像这样的方法，我们叫做拆数法。

　　教师板书“拆数法”。

　　师：我们再来看，它们虽然都用了拆数法，但这过程中又有什么不同的地方？

　　生：①拆了２３，但②却拆了２３和３１。

　　师：也就是说，①对第一个加数进行分拆，②则对两个加数进行分拆，从这里，老师受到了一个启发，能不能对第二个加数进行分拆？猜想一下，行不行？

　　学生大部分说能，有小部分说不能。

　　师：不如我们一起来尝试一下。

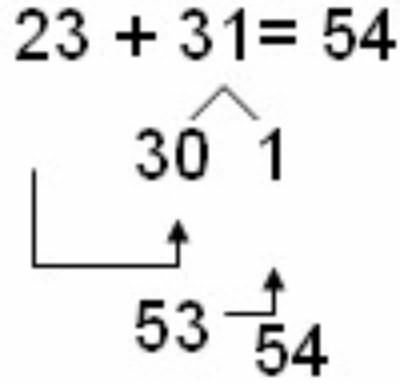
　　教师边引导学生说出分拆的过程，边板书，板书如下：

　　师：结果一样是５４，所以说，拆数法既可以把第一个加数进行分拆，也可以……

　　生齐说：把第二个加数进行分拆。

　　师：更可以……

　　生齐说：两个加数一起分拆。

　　师：好的，不过，我们观察这三条式子。从它们分拆的结果上来看，它们又有什么相同的地方。

　　生：它们都被拆成一个整十数和一个一位数。

　　师：是的，你们很聪明，无论它们拆哪个加数，都把加数拆成整十数和一位数，分拆的目的，就是要把今天所学的《口算两位数加两位数》转化为以前我们学过的《两位数加整十数》和《两位数加一位数》

　　教师在“拆数法”和“两位数加整十数、一位数”中板书符号“→”。

　　师：我们再来看②和③，它们长的不一样，一个是横式，一个是竖式，但从口算的过程来看，能不能找到它们相同的地方？

　　教师竖式上面板书：竖式。

　　生：②和③都是个位数加个位数，整十数加整十数的。

　　师：这位同学眼光非常敏锐。我们一起跟着他的思路来重新看看②和③。②中的３＋１，就是③里面的个位加个位，②中的２０＋３０，就是③里面的十位加十位。虽然它们长的不一样，但却是一伙的，实质都是相同数位上的数相加。

　　教师板书“相同数位上的数相加”。

　　师：③里面的拆数法，目的就是要让相同数位上的数相加。竖式也是一样。

　　教师在“拆数”、“相同数位上的数相加”、“竖式”之间板书两个符号“→”。

　　师：因为今天我们学习的是口算，所以我们先不用研究竖式。②的方法是把加数分拆成整十数和一位数，然后让它们分别相加，③的竖式的排列格式，让两