文/广州市培正中学　菅晓丹

　　可视化工具由于可呈现思考方法和思考路径，在优化教学效果及提升学生思维方面具有一定优势，逐渐成为推动课堂教学改革、实现深度学习的重要载体。笔者从物理过程可视化、物理模型可视化、抽象物理量可视化方面进行探索，呈现完整的动态图景，让学生“经历”整个物理过程，最终促使学生形成扎实的、可迁移的解决实际问题能力，促进学生科学思维发展。 

　　一、画关键位置图，复杂过程可视化 

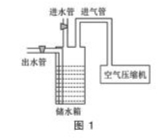
　　例1：如图1所示，某洗车的高压水枪由长方体储水箱、空气压缩机、进气管、进水管和出水管组成，其中水箱的体积为5m3，底面面积为1m2，出水管紧靠水箱顶部。为检测水箱是否漏气，将4m3的水注入水箱，关闭进水管阀门；再用空气压缩机将一大气压下体积为1.4m3空气压入储水箱；打开出水管阀门，查看水箱内剩余水的体积即可判断是否漏气。忽略进、出水管及进气管中气体和水的体积，已知一个大气压相当于10m高的水柱产生的压强，温度保持不变，若水箱不漏气，求剩余水的体积应为多少？ 

　　此题操作过程比较多，有些学生对整个过程的理解看似清楚，实则模糊。一是关闭进水管阀门，竟会认为储水箱是真空；二是打开出水管阀门稳定后，认为此时的气体压强等于外界大气压。 

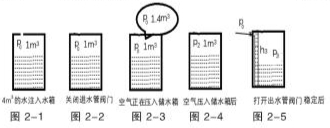
　　教师要给学生留足够的时间画图，让他们“经历”整个操作过程。给水箱注水4m3，如图2-1，此过程水箱与外界连通。注入水后关闭进水管，如图2-2，水箱内密封了一定质量的气体，压强为P0，体积为1m3。用空气压缩机将一标准大气压下体积为1.4m3空气压入储水箱，如图2-3，这是等温情况下的变质量问题。压缩结束后，如图2-4，根据克拉伯龙方程，P0V1+P0?驻V=P2V1得，空气压入后气体压强P2=24mH2O，大于一个标准大气压。打开出水管阀门，水在P2的压力下喷出，稳定后如图2-5，根据图易判断，从空气压入储水箱到打开阀门稳定后，气体质量相同，P2V1=P3Sh3。水不流出时，图2-5内的压强与外界大气压的关系为：P3=P0+ρgh。 

　　联立得h3=2m。显然水箱内剩余水的体积V剩=V总-Sh3=3m3。 

　　根据题目叙述，一步步画出操作过程图，将复杂问题分解为多个熟悉的简单模型，标出每种状态下的P、V和T，轻松跳出陷阱，解决问题。有些学生还可能存在以下疑惑： 

　　质疑一：为什么在研究浇花喷壶、喷洒消毒液时，液面稳定时我们认为内外压强相等呢？ 

　　经对比思考发现，生活用的浇花喷壶产生的高度差约20cm，而洗车储水箱高度为5m，一个标准大气压相当于10m高的水柱产生的压强，所以20cm高的水柱产生的压强完全可以忽略，而储水箱里的水产生的压强显然不能忽略。 

　　质疑二：从图可以看出，从空气压入后到水喷出稳定后的过程中，气体质量都相等，我们能直接对图2-3和图2-5中的状态列理想气体状态方程吗？ 

　　图2-3和图2-5中的气体质量一样，符合理想气体状态方程的适用条件，可以直接列出气态方程求解，多了一种解题方法。 

　　因此，对于多个操作的复杂过程，教师只需要根据题目指引画出一幅幅关键位置图，呈现一个动态的图景，帮助学生理清各个过程的特点及其之间的联系。通过细化过程，提出质疑，解决疑惑，可以剖析更深层次的结构，使物理走向生活，在以后浇花、消毒、洗车的时候，也可以联想到里面包含的物理规律，最终形成可迁移的科学思维素养。 

　　二、无图变有图，物理模型可视化 

　　例2（2021年高考全国乙卷理综第24题）一篮球质量为m=0.60kg，一运动员使其从距地面高度为h1=1.8m处由静止自由落下，反弹高度为h2=1.2m。若使篮球从距地面h3=1.5m的高度由静止下落，并在开始下落的同时向下拍球、球落地后反弹的高度也为1.5m。假设运动员拍球时对球的作用力为恒力，作用时间为t=0.20s；该篮球每次与地面碰撞前后的动能的比值不