（三）因子旋转

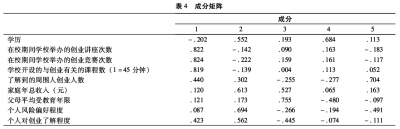
    因子分析的目的不仅是求出公因子，更主要的是知道每个公因子的实际意义，但是由简单估计方法所求出的公因子解，初始因子载荷阵并不满足“简单结构准则”，即各个公因子的典型代表变量不很突出，因而容易使公因子的意义含糊不清，不利于对因子进行解释。为了使因子载荷矩阵中系数更加显著，可以对初始因子载荷矩阵进行旋转，使因子和原始变量的相关系数的绝对值向（０，１）区间的两级分化，从而更容易判断因子意义。

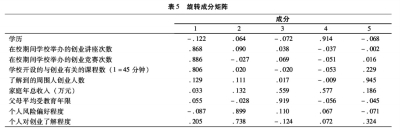
    本文采用的旋转方法是方差最大正交旋转（Ｖａｒｉｍａｘ），即使各因子仍然保持正交的状态，但尽量使各因子的方差差异最大。旋转后的结果如表５。

    由表５可以看出，第一公因子在“在校期间学校举办的创业讲座次数”、“在校期间学校举办的创业竞赛次数”、“学校开设的与创业有关的课程数”有较大的载荷，主要从学校教育方面反映创业的情况，可以命名为“学校创业教育因子”；第二公因子在“个人风险偏好程度”、“个人对创业了解程度”上有较大的载荷，主要从个人的视角反映创业的情况，可以命名为“个人创业素质因子”；第三公因子在“家庭年总收入”和“父母平均受教育年限”有较大的载荷，主要从家庭情况方面反映创业的情况，可以命名为“家庭背景因子”；第四公因子在“学历”上有较大的因子载荷，可以命名为“个人学历因子”；第五公因子在“了解到的周围人创业人数”上有较大的因子载荷，可以命名为“周围创业氛围因子”。

    与旋转之前比，经过旋转之后的各公因子有了更明确的含义，用旋转之后的公因子度量创业情况