初中阶段的新教材中，实际应用问题指的是方程(组)、不等式（组）或者函数在实际生活中的应用问题，本文探讨和研究的范围只包括一次的方程、函数和一元一次不等式或不等式组、反比例函数等知识的实际应用问题，不包括二次方程、二次函数。

　　通过本文的探讨和研究，希望能达到以下两个目标：一、为教师和学生提供一种切实可行的，无论是教还是学，都易于上手操作的解题模式；二、整合各种方程和函数的实际应用问题，把它们统一到同一种通用的分析模式之下，大大地减轻学生的学习负担。切实可行的，易于上手操科作的解题模式究竟是什么样的呢？简而言之，在这样的一个模式的指引下，学生读完题目后，就应该知道首先能做什么，怎么做；接下来又应该做什么，怎么做。就是把整个解题的过程分解成较为固定的，容易上手操作的细小步骤，让大多数学生有可能按照这个指引，把整道题慢慢地“蚕食”掉。这样的一个目标是很有针对性的，因为在实际的教学中发现很多学生读完题目后就显得有点手足无措，但当教师引导他们完成了最初的几步后，他们一般就能自己把剩下的步骤完成，所以学生需要的不是高度概括的总结，而是可行的操作指引。

　　例题是教材向学生输送知识的窗口，学生应该能通过例题理解和掌握相关知识的使用技巧，触类旁通从而达到举一反三的效果。毫无疑问，无论新旧教材里所选的例题都是相当典型的。但在实际使用中发现，不管是解答前的分析，还是解答过程本身，每一道例题基本上是相对独立的，上一道题的分析解答对下一道题并没有产生什么借鉴作用，在这一点上，例题并没有起到让学生触类旁通的作用。

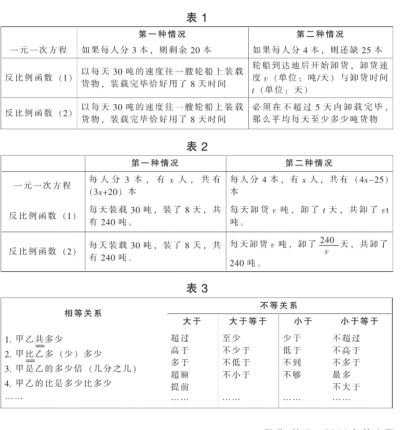
　　在实际教学中，我们发现，大多数的实际应用问题的题目面貌各异，但实质几乎都是一样的。譬如，下面这两道一元一次方程和反比例函数的应用问题：

　　一元一次方程：把一些图书分给某班同学阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本。这个班有多少学生？

　　反比例函数：码头工人以每天30吨的速度往一艘轮船上装载货物，装载完毕恰好用了8天时间。（1）轮船到达地后开始卸货，卸货速度v（单位：吨/天）与卸货时间t（单位：天）之间有怎样的函数关系？（2）由于遇到紧急情况，船上的货物必须在不超过5天内卸载完毕，那么平均每天至少多少吨货物？

　　从两个方面来进行比较我们就可以看出它们的类似之处：

　　（一）从每个问题的的结构上来看，它们都叙述了两种情况。（见表1）

　　(二)从每种情况所涉及到数量来看，它们都用到了三个数量，而且这个三个数量中一般有一个是