数形结合，指的是数与形之间的一一对应。通过”以数解形”或“以形助数”，即通过抽象思维与形象思维相结合，使抽象问题具体化，复杂问题简单化，从而优化解题途径。 数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休。”可见数形结合的数学思想十分重要。

　　通过深入研读教材，我认为《乘法分配律》的教学还可以运用案例教学法渗透数形结合的思想。

　　我设计了一个案例，以微课的形式呈现这个现实生活的情景的案例：“小红家的果园由连在一起的一块长方形的荔枝林和一块长方形的龙眼林组成，（可画出如下示意图），小红家的果园有多大？”通过呈现这个现实生活中的数学案例，引导学生独立思考。

　　学生列出：(33+67)×22和33×22+67×22

　　第一种是合并式思考的方法，求100个22是多少。第二种用了分解式思考，33个22加上67个22是多少。学生完成后问：哪种方法较好？

　　这样，运用案例教学法，结合解决实际问题的过程，理解乘法分配律的含义，培养解决生活中相关实际问题的能力，渗透了数形结合思想和多样化择优的思想。

　　三、运用案例教学渗透转化思想

　　转化的数学思想方法将某些已知条件或数量关系转化为另外的条件或关系,化新知为旧知、化繁为简、化难为易的一种数学思想方法。相对其他教学法而言，运用案例教学法渗透转化的数学思想方法则别有新意。下面以《鸡兔同笼》为例，探讨如何运用案例教学渗透转化的数学思想方法。

　　人教版新教材四年级下册的“数学广角”内容中出现的鸡兔同笼问题难度降低：笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚。鸡和兔各几只？

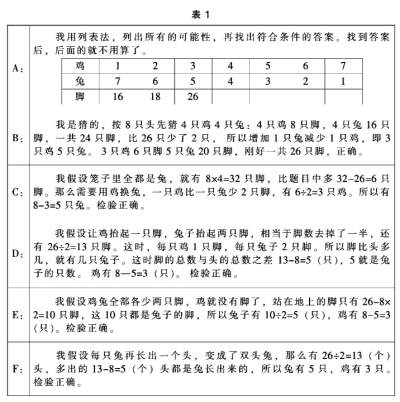
　　为了使学生很好地理解，我用动画设计了微课形式的教学案例，在学生独立思考并讨论后，播放《鸡兔同笼》案例。先呈现鸡兔同笼的题目动画形象与问题：笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚。鸡和兔各几只？  几个小朋友(以下分别用A\B\C\D\E\F\代替)围在旁边，各自思考，各抒已见。（见表1）

　　在这个案例的各位孩子的讨论中，无论哪一种假设法都是用了不同形式的转化，巧妙的转化还显示了其解法的优越性，而这些转化均体现了同一种数学思想——化归思想，还渗透了对应思想与变中抓不变的思想方法。通过转化，灵活地解决了问题。这个案例数据简单，呈现形式生活化；通过重视双边互动教学，在学生独立思考后再播放呈现，避免了学生不思考直接等答案，培养了学生独立思考的能力。运用这个案例，再解决1500年前《孙子算经》中：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何?这四句话的意思是:有若干只鸡兔同在一个笼子里，从上而数，有35个头;从下而数，有94只脚。求笼中各有几只鸡和兔? ”此类数据较大的题目就得心应手；学生也能举一反三，解决其他相关的问题也水到渠成。

　　【本文为广州市教育科学规划2017年度市一般课题“基于核心素养的小学学科案例教学研究”（课题编号1201730069）的成果之一】

　　责任编辑　龙建刚