例题.（2016全国I理）已知函数f（x）=（x-2）ex+a（x-1）2有两个零点，求的取值范围。

　　本题考查函数的零点问题，可以将其转化为方程思想来解，也可以从零点的几何特征转化为两个函数的图像的交点问题来处理。

　　解法一：分类讨论法。分类讨论是将数学问题按某个方向进行分类，然后将每一类分别进行研究，最后整合，分类讨论的基本思路是化整为零，逐个突破。

　　当a=0时，f（x）=（x-2）ex，由  f（x）=0解得x=2，则f（x）只有一个零点，不符合题意。

　　当a＞0时，■=（x-1）(ex+2a)，令■=0解得x=1，所以x∈（-∞，1）时，f'（x）＜0；x∈（1， +∞）时，f'（x）＞0。函数f（x）在 （-∞，1）上单调递减，在（1，+∞）上单调递增。从而f（x）≥f（1）=-e，由f（2）=a＞0，则函数f（x）在（1，+∞）上有一个零点；由■f（x）=+∞，则f（x）在（-∞，1）上有一个零点。所以函数f（x）有两个零点。

　　类似地证明可以得出当a＜0时f（x）不可能有两个零点。（过程略）

　　综上所述，实数a的取值范围是（0，+∞）。

　　解法二：数形结合法。函数   f（x）的零点，即函数f（x）的图像与x轴的交点的横坐标，是数形结合思想应用的联结点，因此用图像来揭开函数零点的神秘面纱成为解决函数零点问题常用有效的方法。

　　令f（x）=0，即（x-2）ex+a（x-1）2=0，可知x-1≠0，得a（x-1）=■。函数f（x）有两个零点转化为f'■（x）=a（x-1）的图像与f'2（x）=■的图像有两个不同交点的问题。

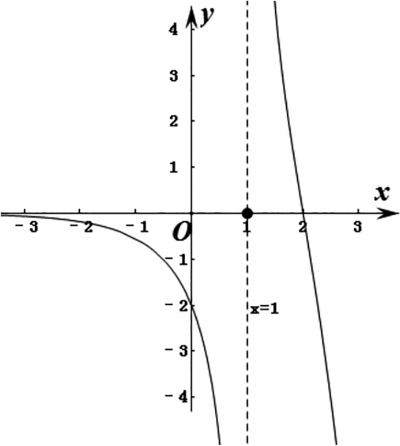
　　由■=■(x≠1)， f'2（x）=■，因为-x2+3x-3＜0，所以f'2（x）＜0，即f2（x）在（-∞，1）和（1，+∞）上都单调递减。又■f2（x）=0，■f2（x）=-∞，■f2（x）=   +∞，■f2（x）=-∞，作出函数f2（x）的图像如图1所示。

　　f1（x）=a（x-1）的图像是过定点（1，0）的直线，要使■的图像与f2（x）的图像有两个不同交点，由图1可知，直线f1（x）的斜率a＞0。

　　解法三：参变分离法。参变分离法，也即将原函数中的变量和参量进行分离后变形为■=h（x），将原函数的零点问题化归为与x轴平行的直线y=g（a）与函数h（x）的图像的交点问题。巧用参数分离求函数零点问题，可以回避对参数取值范围的分类讨论，又形象直观。

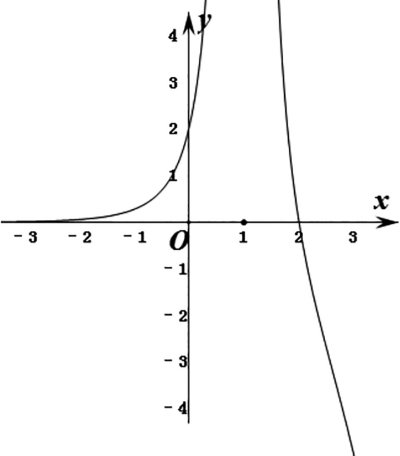
　　令f（x）=0，即（x-2）ex+a（x-1）2=0，可知x≠1，则a=■，记  h（x）=■，则■=■。由于-x2+4x-5＜0，所以x∈（-∞，1）时，h'（x）＜0；x∈（1，+∞）时，h'（x）＞0。又因为■h（x）=0，■h（x）=+∞，■h（x）=-∞，作出函数h（x）的示意图如图3所示。

　　移动直线y=a，结合图像，要使a=■有两个不同实根，可知a＞0。

　　本题反思：由本题的三种方法，可知解决含参零点问题常用方法可概括为三种。

　　一、带参讨论法：当无法通过等价转化的思想将原问题化归为相对容易的问题，此时根据题设要求地对参数的取值进行分类讨论，逐一求解。利用该策略求解时一般要求明确讨论的标准，并且做到不重不漏。如解法一中既要考虑a的正负对函数■的零点个数的影响，当a＜0时，还要比较函数f（x）的两个极值点1与■的大小关系。

　　二、数形结合法：由两个基本初等函数组合而得的函数■=g（x）-h（x）的零点个数，等价于方程g（x）-h（x）=0的解的个数，也即g（x）=h（x）的解的个数，进而转化为基本初等函数y=g（x）与y=h（x）的图像的交点个数。

　　三、参变分离法：通过将原函数中的变量和参量进行分离后变形为g（a）=h（x），则原函数的零点问题化归为与轴平行的直线y=g（a）与函数h（x）的图像的交点问题。

　　责任编辑　徐国坚