存在性探究题是指在一定的条件下，判断某种数学对象是否存在的问题，它有结论存在和结论不存在两种情形．解答这类问题，一般先假设所探究的对象已知存在，然后建立适当的数学模型（如函数、方程、不等式等），运用一定的数学思想方法（如数形结合、分类讨论等），通过计算或推理，如果探究出与条件相符号的结果，则说明假设成立，并由此得出问题的结论；否则就不存在．

　　一、存在直线与抛物线只有一个点

　　例１：已知点A（-1，-1）在抛物线y=(k2-1)x2-2(k-2)x+1是上．（1）求抛物线的对称轴；（2）若B点与A点关于抛物线的对称轴，问是否存在与抛物线只交于一点B的直线？如果存在，求符合条件的直线；如果不存在说明理由．

　　思路点拨：①用待定系数法求抛物线的解析式；②根据抛物线的对称轴公式求对称轴，或用配方法求对称轴；③由对称轴的性质求出点A关于x=- 的轴对称点B的坐标；④求点的坐标转化为求过点B直线的解析式与抛物线的解析式组成方程组的解，但别忘了过B点平行于y轴的那条直线．

　　二、存在直线与直线平行（或垂直）

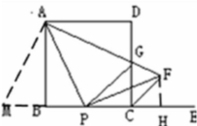
　　例2：（2009上海中考）如图，已知在正方形ABCD中，AB=2，P是边BC上的任意一点，E是边BC延长线上点，连结AP.过点P作PF⊥AP，与∠DCE的平分线CF相交于点F.连结AF，与边CD相交于点G，连结PG.（1）求证：AP=FP；（2）⊙P、⊙G的半径分别是PB、GD，试判断⊙P与⊙G两圆的位置关系，并说明理由；（3）当BP取何值时，PG∥CF.

　　思路点拨：①先证△ABP∽△PNF,再证△ABP≌△PNF; ②作辅助线，证△APM≌△APG;③由平行线的性质及等腰直角三角形的性质，由（2）的数量关系PG=BP+GD，建立方程求解．

　　三、存在直线与圆相切

　　例3：（惠州市中考试题）已知：如图（图略），抛物线y=- x2- x+ 的图像与x轴分别交于A、B两点，与y轴交于C点，⊙M经过原点O及A，C，点D是劣弧OA上一动点（D点与A，O不重合）.（1）求⊙M的面积；（2）连接CD交AO于点F，延长CD至G，使FG＝2，试探究当点D运动到何处时，直线GA与⊙M相切，并请说明理由.

　　思路点拨：①求圆的面积关键是求圆的半径；②由直线与圆相切的知识，猜想点D是弧AO的中点，由点D是弧AO的中点证明直线GA与⊙M相切.

　　四、存在特殊三角形（等腰三角形、等边三角形、直角三角形、等腰直角三角形）

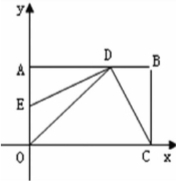
　　例4：（2009重庆市中考）已知：如图，在平面直角坐标系xoy中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3，过原点O作∠AOC的平分线交AB于点D，连结DC，过点D作DE⊥DC，交OA于点E.（1）求过点E、D、C的抛物线的解析式；（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G.如果DF与（1）中的抛物线交于另一点M，点M的横坐标为 ，那么EF=20G是否成立？若成立，请给予证明；若不成立，请说明理由；（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由.

　　思路点拨：①用待定系数法求抛物线的解析式，这个解析式在第（2）、（3）题的计算中要用到；②过点M作MN⊥AB,根据对应线段成比例可以求FA的长；③将∠EDC绕点D旋转的过程中，△DCG与△DEF保持全等；④第（3）题反客为主，分三种情况讨论△PCG为等腰三角形，根据点P的位置确定点Q的位置，再计算点Q 的坐标.

　　五、存在特殊四边形（平行四边形、矩形、菱形、正方形、梯形）

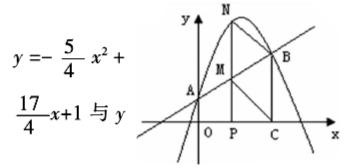
　　例5：（2011广东中考）如图，抛物线y=- x2+ x+1与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）.（1）求直线AB的函数关系式；（2）动点P