评析：本题是代数与几何的综合运用，解题时应多角度、多线索深入分析，灵活运用数形结合的思想、数学建模的思想、分析讨论的思想、转化的思想、待定系数法等多种数学思想与方法．

　　六、存在三角形相似

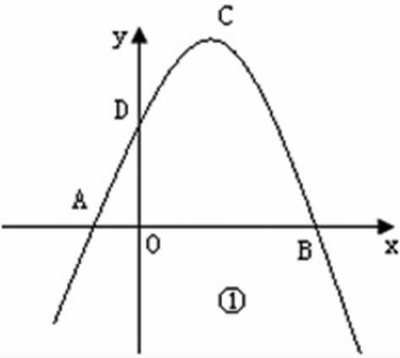
　　例6:（2011深圳市中考）如图①，抛物线y=ax2+bx+c(a≠0）的顶点为C（1，4），交x轴于A，B两点，交y轴于点D，其中点B的坐标为（3，0）.（1）求抛物线的解析式；（2）如图②（图略），过点A的直线与抛物线交于点E，交y轴于点F，其中点E的横坐标为2，若直线PQ为抛物线的对称轴，点G为直线PQ上的一动点，则x轴上是否存在一点H，使D、G、H、F四点所围成的四边形周长最小.若不存在，请说明理由；（3）如图③（图略），在抛物线上是否存在一点T，过点T作x轴的垂线，垂足为点M,过点M作MN∥BD，交线段AD于点N，连接MD，使△DNM∽△BMD，若存在，求出点T的坐标；若不存在，请说明理由．

　　评价：本题考查学生二次函数与四边形、相似三角形等几何知识的综合运用能力．  

　　七、存在相等距离（或相等面积、等周长、定值）

　　例7：（2009上海市中考）二次函数y=- x2+bx+c的图像经过点A（4，0）、B（-4，-4），且与y轴交于点C.（1）试求此二次函数的解析式；（2）试证明：∠BAO=∠CAO（其中O是原点）；（3）若P是线段AB上的一个动点（不与A、B重合），过P作y轴的平行线，分别交此二次函数图像及x轴Q、H两点，试问：是否存在这样的点P，使PH=2QH？若存在，请求出点P的坐标；若不存在，请说明理由．

　　思路点拨：①用待定系数法求二次函数的解析式；②数形结合，求∠BAO与∠CAO的正切值，可以判定∠BAO=∠CAO；③分类讨论PH=2QH，根据点Q的位置分两种情况；④利用典型题目的结论，把PH=2QH时点，Q的位置转化为OD、OC的中点问题．

　　八、存在最大值（或最小值）

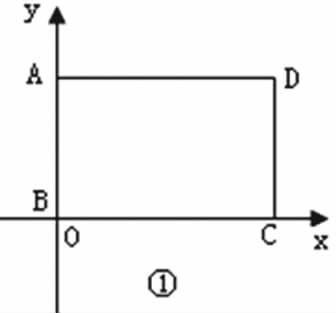
　　例8： （2011陕西中考）如图①，在矩形ABCD中，将矩形折叠，使点B落在边AD（含端点）上，落点记为E，这时折痕与边BC或边CD（含端点）交于点F．然后再展开平铺，则以B，E，F为顶点的△BEF称为矩形ABCD的“折痕三角形”. （1）由“折痕三角形”的定义可知，矩形ABCDD的任意一个“折痕△BEF”一定是一个　　 三角形；（2）如图②（图略），在矩形ABCD中，AB=2，BC=4.当它的“折痕△BEF”的顶点E位于边AD的中点时，画出这个“折痕△BEF”，并求出点F的坐标；（3）如图③（图略），在矩形ABCD中，AB=2，BC=4.该矩形是否存在面积最大的“折痕△BEF”？若存在，说明理由，并求出此时点E的坐标；若不存在，为什么？

　　评析：本题考查学生的阅读理解及图形的操作能力，首先阅读题意，理解最基本的概念“折痕三角形”，然后利用此概念解决有关问题，此过程中画出满足题意的图形是解决问题的关键，然后根据图形，分析出数量关系从而解决问题．

　　九、“不存在”的问题

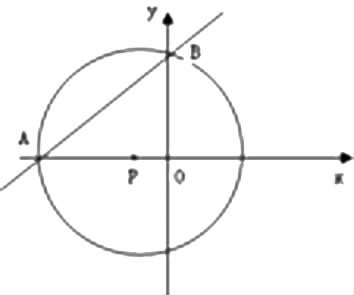
　　例9：（2009上海中考）如图，在平面直角坐标系中，直线y=kx+b分别与x轴负半轴交于点A，与y轴正半轴交于点B，⊙P经过点A、点B（圆心P在x轴负半轴上），已知AB=10，AP= .（1）求点P到AB的距离；求直线y=kx+b的解析式；（3）在⊙P上是否存在点Q，使以A、P、B、Q为顶点的四边形是菱形？若存在点Q，使A、P、B、Q对顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，并说明理由．

　　思路点拨：①求点P到AB的距离要用到垂径定理和勾股定理；②求直线的解析式的前提是求点A、B的坐标，求点A、B的坐标的关键是解直角三角形AOB；③以AB为对角线或者分类讨论菱形的存在性，当AB为对角线时，两条对角线不互相平分；当AB为边时，两邻边不相等．

　　存在性题型的考察，是对学生对所学数学知识的全面综合的检测，它考察的是学生的分析问题、解决问题的能力，考察学生对所学知识的灵活运用，考察的是学生的学科综合素质．因此，我们的日常的教学中，除了做好双基的教学工作外，还应注意抓好学生的数学意识和数学基本思想以及数学基本能力的培养．

　　责任编辑 罗 峰