下面，探究初中数学九年级上册的第1课时《菱形的性质》运用SOLO分类评价法在教学的应用。（这里只展示两个环节，即“预习案”和“学习案”）

　　本课的核心目标：理解菱形的概念，掌握菱形的性质并能应用这些知识进行有关的计算和证明。我们运用SOLO分类设置问题，在“预习案”的【课前导学】设置为：

　　阅读课本P2-P4，完成下列内容。

　　1. 菱形的定义：有一组　　的平行四边形叫做菱形。

　　2. 探索菱形的性质：由定义可知，菱形是特殊的平行四边形，所以它具有平行四边形的一切性质，但又有自己的独特的性质。填写下表：

　　3. 在菱形中，连接两条对角线后，你能发现哪些特殊的三角形？各有几个？

　　4. 根据菱形中出现的特殊三角形，我们在解决问题时，会用到的知识点可能有哪些？

　　单点结构层次是问题1，多点结构层次是问题2，关联结构层次是问题3，拓展抽象结构层次是问题4. 学生在自主预习中去理解菱形的定义以及菱形的性质，把菱形的特征对比平行四边形的特征，并能发现异同点，对一些思维层次高的学生进一步发现菱形的是由一些特殊的三角形构成，在解决问题时能把这些特殊的三角形性质综合运用，这样在预习中让各层次的学生都能发挥自己的数学思维，到达自主学习的目标。

　　【尝试练习】1. 菱形具有而一般平行四边形不具有的性质是(　)

　　A. 对角相等

　　B. 对边相等

　　C. 对角线互相垂直

　　D. 对角线互相平分

　　2. 菱形的周长为20㎝，它的边长为　　。

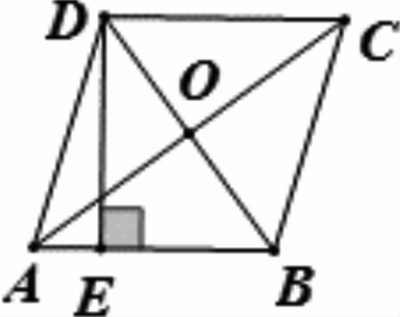
　　3. 如图3，已知在菱形ABCD中，AC与BD相交于点O，AC=24，DB=10，

　　（1）菱形的边长为　　，周长为　　。

　　(2)试求菱形的面积。

　　【尝试练习】设置三个题目，为不同层次的学生提供不同水平的问题，那么老师在上课前了解学生的学习结果，区分学习结果的层次也就一目了然，而且更加清楚地显示学生对某个问题的认知水平，也为师生提供有关教学质量的信息，这样的思维层次有利于教师制定教学目标，为在课堂上解答学生的疑难问题更加准确到位，大大提高了课堂效率。

　　“学习案”是课堂的质量和效果的保证，本环节设置衔接“预习案”的内容，进一步把问题深化、拓展、延伸，本环节设置为：

　　【知识点拨】1. 由菱形是轴对称性图形，可以直观理解它的性质；

　　2. 运用菱形的性质，结合等腰三角形性质或勾股定理解决问题。

　　【课内训练】

　　1. 下列图形中，不是轴对称图形的是（　　）

　　A. 等腰三角形

　　B. 平行四边形

　　C. 角 

　　D. 菱形

　　2. 如图4，菱形ABCD中∠DAB=60°，则∠ABD=　　。

　　3. 边长为4的菱形，它的一个内角等于60°，则菱形的两条对角线的长度分别为　　、。

　　4. 如图5，在菱形ABCD中，AC和BD是两条对角线，

　　(1)若AB=6㎝，则BC=　，周长为　　。

　　（2）若∠ABC=40°则∠BAD=　，∠ABD=　　，∠BAC=　　。

　　5. 如图6，在菱形ABCD中，AC和BD相交于点O，AC=8，BD=6。

　　（1）求菱形的边长；

　　（2）求菱形的面积；

　　（3）求菱形的高DE。

　　【课内训练】问题1是单点结构层次，学生对轴对称概念理解就可以回答的，问题2是多点结构层次，学生要理解菱形的定义和等腰三角形的性质才能回答，问题3、4是关联结构层次，用到的知识有菱形的定义和性质、等腰三角形的性质、勾股定理等，问题5是前几个结构层次的综合。课堂是面向全体学生，分层递进，让全体学生都能参与课堂学习，运用SOLO分类的理论指导课堂，更加明确学生的思维水平，更利于培养学生学习的积极性和主动性。

　　四、SOLO分类评价的优越性

　　在教学中不断渗入SOLO分类的评价法，前面只是尝试在讲授新课的探究，SOLO评价更应该在复习课中进行，这样有助于对学生的思维层次的划分；有助于教师教学的目标实现；有助于教师进行教学效果的检测；有助于为高思维能力的学生提升得更高更快；有助于对学生的评价深入到了质的层面，从而达到新课程教学改革的目的，更为教学质量的提升提供多一个渠道。

　　责任编辑 徐国坚