数学教学是数学活动的教学，是师生之间，学生之间交往互动与共同发展的过程。数学教学应从学生实际出发，创设有助于学生自主学习的问题情景，引导学生通过实践、思考、探索、交流，获得知识，形成技能，发展思维，学会学习，促使学生在教师指导下生动活泼地、主动地、富有个性的学习。《课程标准》指出，既要关注学生的学习结果，也要关注学生的学习过程，特别是对学生的思维过程的评价给予更多的关注。而如何评价学生的思维水平呢？SOLO分类法能较好地解决这个问题。

　　SOLO是英文“Structure of the Observed LearningOutcome”首字母的缩写，意为“可观察到的学习成果的结构”。SOLO分类理论将学生思维层次由低到高分为五个不同的层次，即前结构、单点结构、多点结构、关联结构、拓展抽象结构等。

　　1. 以《平行线分线段成比例》的教学片断为例

　　课堂上应当提供机会让学生表达自己的思考，尊重学生的想法，注重学生思维能力的培养，在课前的教学设计中预设有利于促进学生的问题，但也要分析学生在课堂上的应答，重视学生应答的生成资源。学生的表达被认真聆听，学生的学习热情才能被保护，学习的愿望才能驱使学生良性的学习循环。

　　在一节《平行线分线段成比例》的公开课上，在讲定理之前，作为铺垫，教师先介绍了平行线等分线段定理：

　　已知：直线a∥b∥c，AB=BC．求证：DE=EF．

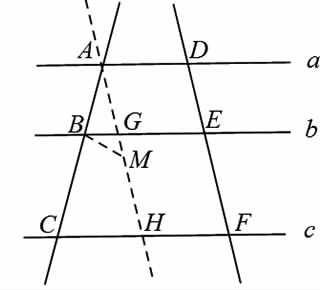
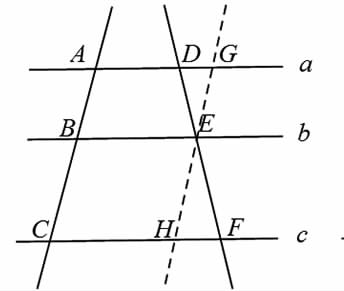
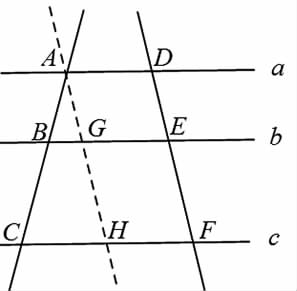
　　当老师询问同学们如何证明后，有学生提出了过点A作DF的平行线，如图1，但老师没有理会，只是告诉学生“你错了”，然后在图上作出图2的辅助线，接着在黑板上工整地板书出很完美的过程，主要思路是利用平行四边形对边相等，加上“对顶角相等”，得到?驻DEG≌?驻FEH，最后得到DE=EF。

　　当老师板书完毕，学生再次提出了自己的观点，但老师还是坚决地告诉他：“你错了。”在双方的坚持中，当老师第五次告诉这位同学“你错了”之后，以老师的一句“我们下课后再讨论，好吗？”而告终。

　　老师胜利了，一堂课的教学内容也完成了。下课后我找到那位同学，请他给我讲解一下他的思路。该生在图中画出辅助线并开始陈述他的想法。

　　如图3，取线段AH的中点M，因为B为线段AC中点，则BM为?驻ACH的中位线，所以BM∥CH，又BG∥CH，而根据平行公理，过一点有且只有一点与已知直线平行，所以点M、G重合，即点G为AH的中点，从而可得到原题结论。

　　这位同学的想法让人眼前为之一亮，说实话，笔者也没想到利用同一法的思想。后来笔者又与那位老师沟通，问他为什么那么肯定地认为学生的想法是错的，原来他以为这位学生的思路是由B为线段AC中点以及BG∥CH，立即就得到G为AH的中点的结论，估计他是与中位线混淆。老师也表明了当时是怕教学内容处理不完，所以没让同学解释，课后会找那位同学沟通的。

　　听完课后，笔者不禁思考“该同学以后上课还会不会提出自己的观点，积极地思考问题呢？”新课程要求在教学活动中，教师应发扬教学民主，成为学生数学活动的组织者、引导者、合作者；要善于激发学生的学习潜能，鼓励学生大胆提出自己的观点与见解。而在实际教学，有多少教师利用“教学机智”将学生拉到自己预设的轨道上来，使得课堂教学按照原先的设定完成了既定任务。看似“完美”，可是这“完美”实际上在慢慢泯灭学生的创造性，这是一种虚假的教学机智，真正的教学机智要有对学生提出问题的尊重，而不是把学生的智慧当作实现教师课堂预设的垫脚石。但从SOLO分类理论的角度来看，这位同学的思维层次已经达到了拓展抽象结构层次。他通过同一法，并运用平行公理来解决新的问题，对所学知识进行灵活的运用。学生是否具备思考问题的方式远比他们一节课接受了多少内容来得更为重要，当我们换一种评价方式去看学生，这种导向作用最终一定激励学生进行深层次的思考，形成良性循环，从而可以培养出更多的敢于提出问题，敢于思考的人