动点问题涉及的知识点多，蕴含的数学思想方法集中，能全面考查学生获取数学信息以及数学思想方法分析问题和解决问题的能力。本文以2014年广东中考最后一道动点问题为例，对个人课堂创新教学片段进行分析思考整理，供同行参考。

　　一、谋攻篇，题型分析

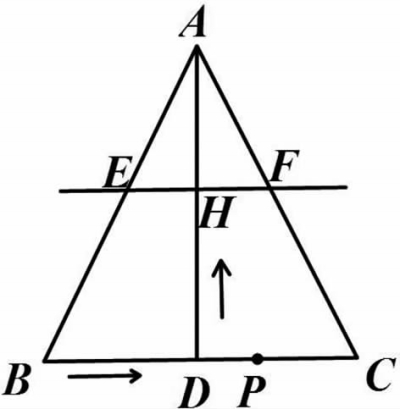
　　例题：如图1，在△ABC中，AB=AC，AD⊥BC点D，BC=10cm，AD=8cm，点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t＞0）。

　　（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形；（2）在整个运动过程中，所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长；（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值，若不存在，请说明理由。

　　1. 纵观全局，胸有成竹

　　此题第（1）题中EF在运动变化过程总能得到四边形AEDF的一般性结论，由此再去探讨它的特殊性，即四边形AEDF为菱形，而在整个探讨的过程发现点E、F、D分别是△ABC各边的中点这一特殊性。在整个运动变化过程中始终不变的还有△AEF∽△ABC的一般性的特征。再由此去研究第（2）题面积的特殊性，即△PEF的面积的最大值这一特殊性，以及第（3）题△PEF形状的特殊性。

　　2. 分析思路，组方杀题

　　学生A：第（1）题是通过E、F、D分别是△ABC各边的中点，可以用中位线定理来证明得出DH=AH、 EH=FH进而证明四边形AEDF为菱形。

　　教师引：合理的转化可以快速的形成解题思路，兵法称“围魏救赵”，我们要懂得转个弯思考解决问题。  

　　学生B ：第（2）题为了得出△PEF的面积的最大值，关键是要得到△PEF的面积公式S△PEF =■EF·h，而公式的关键在于找高h，而高h会不会是DH的值？

　　教师引：你的想法很好，如果公式S△PEF =■EF·DH成立，那公式是怎么得到，有没有哪个同学知道？

　　学生C：第（2）题我也认为公式成立，但理由也是说不出来，可是我能得到DH=2t，EF=10-■t。

　　教师引：你是怎样做到的？

　　学生C：由DH=2t，可得AH=8－2t，由EF∥BC知△AEF∽△ABC。又因为BC=10cm，AD=8cm，∴■ =■即■=■，解得EF=10-■t。

　　学生D：第（3）题若△PEF为直角三角形，显然就要思考先寻找EP2，FP2，EF2的值，而寻找EP2，FP2，EF2的值又应该跟勾股定理有关系，而勾股定理则要有直角三角形方可破解，而原图显然条件不充分，这时，该如何构建直角三角形？能不能添加辅助线？

　　教师引：添辅助线兵法称“借刀杀人”，借得好，就成功一半。

　　学生E：如果“借刀杀人”成功的话，那么，寻找EP2、FP2、EF2的值就能转化成分别获取与EP2、FP2、EF2相关的线段含t的代数式，这样一来就可以将其代人化难为易，最后用勾股数组去探讨△PEF为直角三角形时，求t值的情况。也就是题（3）可以利用勾股定理去构建等式，如EP2=（）2+（）2=？，FP2=（）2+（）2=？，EF2=（）2+（）2=？然后再去化简。

　　学生H：第（3）题，不用添加辅助线同样可以求出t值。通过△PEF的三个内角分别为直角时展开分类讨论，进行取舍t值，分三种情况讨论： ①若∠FEP=90°，则……②若∠EFP=90°，则……③若∠EPF=90°，则利用三角形相似和勾股定理就能解决问题。

　　二、虚实篇，化险击破

　　通过题型分析，题中险阻就充分暴露出来。主要有以下两点：学生困惑1，△PEF的高为何是DH的值？学生困惑2，构建直角三角形找EP2、FP2、EF2的值，这辅助线该如何添？当学生在分析问题遇到困阻时，课堂活动则应由学生尝试分析问题为主过渡到以教师分析讲解为主，让学生在分析问题受困之处，有例可仿、有境可生，达到实现“知彼”。《孙子兵法》云：胜可为也。也就是说在分析问题思路受困时，往往需要添辅助线“借刀杀人”。

　　责任编辑 徐国坚