二、从圆出发，构建基本图形

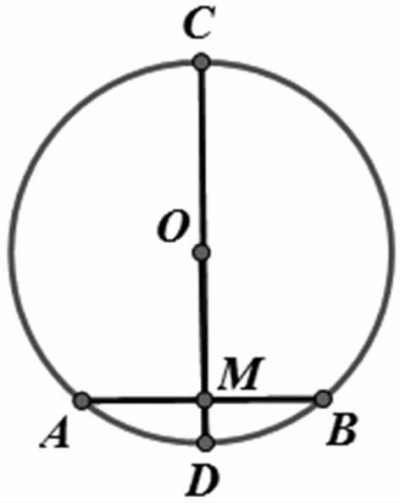
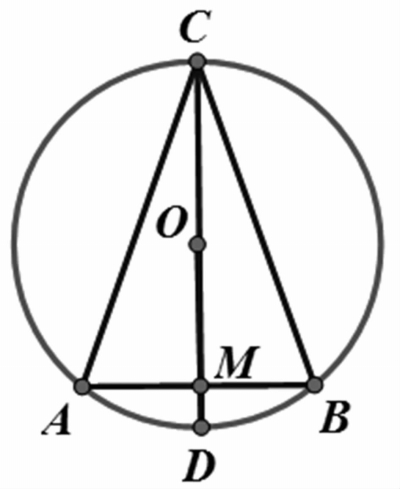
　　例2：如图5，AB是⊙O的弦，CD是⊙O的直径，CD=15，CD⊥AB于点M，如果sin∠ACB=  ■ ，求AB的长。

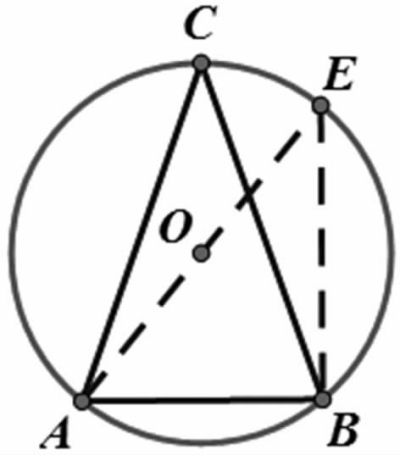
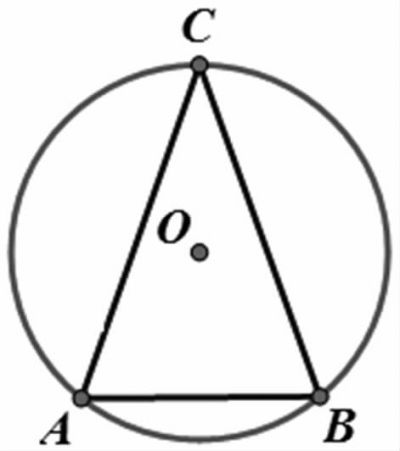
　　分析：（方法一）因为∠C是圆周角（如图6）且已知圆的直径等于15，要求弦AB 的长，则考虑连AO并延长交⊙O于点E，利用直径所对的圆周角是90°构造Rt△ABE（如图7），得∠E=∠C，∵sin∠ACB=■，∴sin∠AEB=■，可求AB=9。

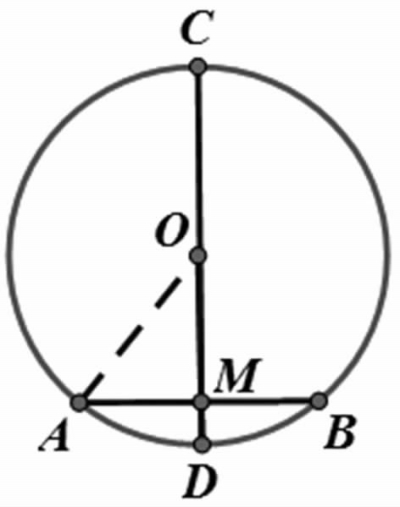
　　（方法二）由直径CD⊥AB于点M，联想垂径定理的基本图形（如图8），可以连接AO构造Rt△AOM，可得圆心角∠AOM等于圆周角∠ACB（如图9），于是sin∠AOM=sin∠ACB = ■，所以■=■，可求AM=■，得AB=9。

　　评注：有时候拆分了复杂几何图形，可能只是得到了某些基本图形的一部分，尚不足以解决问题的时候，要通过添加相应的辅助线来构造基本图形，此类构造要紧紧围绕相关定理、性质的模型展开联想。

　　三、数形结合，各司其职

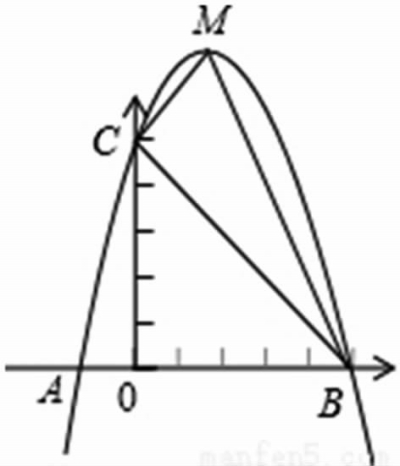
　　例3：如图10，已知，二次函数y=ax2+bx+c的图像与x轴交于A、B两点，其中A点坐标为（-1,0），点C（0,5），另抛物线经过点（1,8），M为它的顶点。

　　（1）求抛物线的解析式；

　　（2）求△MCB的面积S△MCB。

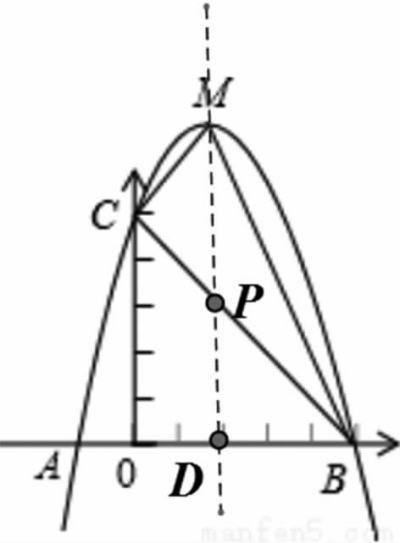
　　分析：（方法一）（1）由一般式易求二次函数解析式y=-x2+4x+5，因此可求顶点M（2,9）及抛物线与X轴另一个交点B（5,0）；（2）如图11画出抛物线的对称轴直线X=2，交BC于点P，交X轴于点D（2,0），求BC所在直线解析式为y=-x+5，所以点P坐标是（2,3），以MP为底，图分别以OD、OB为高求△MCP和△MBP的面积，两个三角形的面积之和就是△MCB的面积，所以S△MCB=■×MP×OD+■×MP×DB=■×MP×(OD+DB)= ■×6×5=15。

　　评注：此为综合法，在解题的过程中没有拆复杂图形为基本图形，观察△MCB的时候易受到抛物线的干扰，学习处理起来综合难度高，解答较为困难，而且在实际解题时候并不容易发现三角形面积与函数模型及坐标系之间的联系。

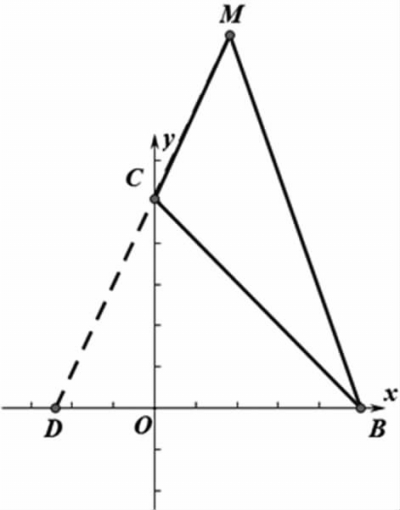
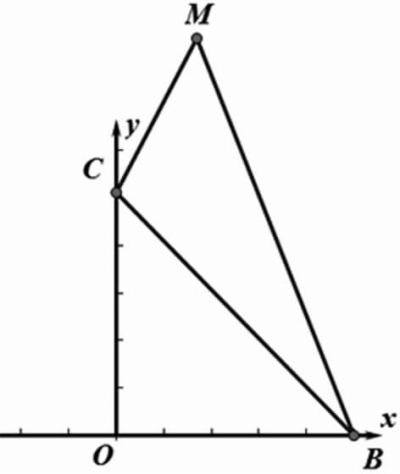
　　分析：（方法二）因为△BCM与抛物线只有公共点B、C、M，求△MCB的面积，可考虑求出顶点M的坐标（2,9）和与X轴交点B（5,0）后抹去抛物线，即分离图形，如图12，只留下平面直角坐标系和△BCM。如图13，延长MC交X轴于点D，求直线MC解析式为y=2x+5，得点D（-■,0），所以S△MCB=■×DB×9-■×BD×CO=■×■×9-■×■×5=15。

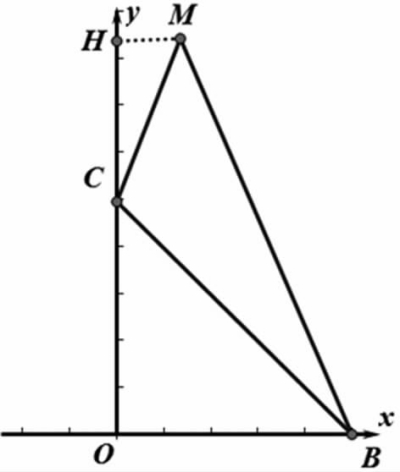
　　（方法三）分离图形同方法二，如图14，作MH⊥y轴于点H，得H(0,9），则△MCB的面积等于梯形MHOB的面积减去△OCB和△MHC的面积。

　　总之，分解出组合图形中的基本图形，运用多种方法解决同一个问题，开拓了学习者的思维能力，发展了空间想象能力，通过基本图形联系数学与外部世界，渗透数学学习中的三个基本思想，即抽象、推理和模型。教师在教学中要有意识地强化对基本图形的运用，不断地运用基本图形去发现、描述问题，理解、记忆结果。谁能把图形的内涵挖掘的深一些，谁的“拆分、整合”就灵活些，相应的解题思路就多些，如此坚持下去，解题能力就会不断提高。

　　责任编辑 韦英哲