通过对较复杂图形进行分解或者重新构建，减少背景图形对问题的干扰，提取有效信息解决问题，是处理较复杂图形时比较有效的方法。

　　一、相似中的基本图形

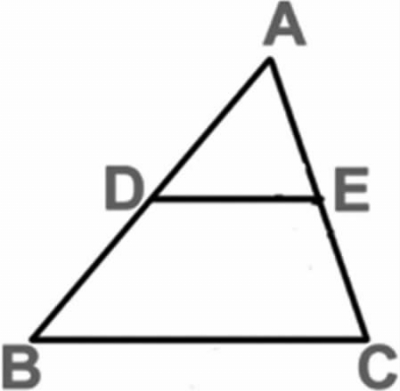
　　如图1，A字型是两个三角形相似的基本图形之一，当DE∥BC时即有△ADE∽△ABC 。

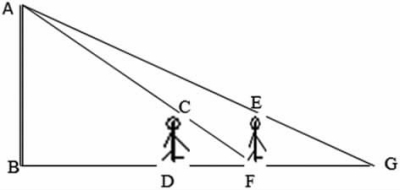
　　例1：如图2，有一路灯杆AB，在灯光下，小明在点D处测得自己的影长DF＝3m，沿BD方向到达点F处再测得自己得影长FG＝4m，如果小明的身高为1.6m，求路灯杆AB的高度。

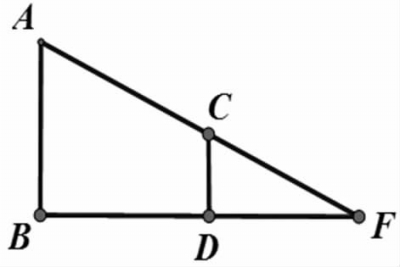
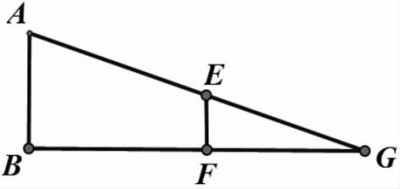
　　分析：此图中包含了两个A字型图形，如图3、图4，即△FCD∽△FAB和△GEF∽△GAB，针对此类复杂图形，整体观察较难发现其中隐含的关系，如果对图形进行拆分、观察，分别整理出对应的比例关系，寻找两组比例关系中的共性与区别，则易求路灯杆AB的高度。

　　解:由△FCD∽△FAB得■=■, 由△GEF∽△GAB得■=■，∵小明的身高为1.6m，∴CD=EF=1.6，∴■=■，∴■=■,又∵DF＝3m，FG＝4m，且BG=BF+4，∴■=■，解得BF=12 m，再带入■=■，得■=■解得AB=6.4 m，即路灯杆AB的高度是6.4 m。